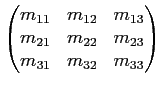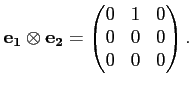Plaçons nous dans
 R3 et considérons un tenseur
R3 et considérons un tenseur
 M d'ordre 2, c'est à dire un champ défini sur une partie
Ω de
M d'ordre 2, c'est à dire un champ défini sur une partie
Ω de
 R3 et à valeur dans
R3 et à valeur dans
 (
( R3), l'ensemble des opérateurs linéaires sur
R3), l'ensemble des opérateurs linéaires sur
 R3.
R3.
Ainsi, si
(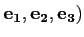 désigne la base
canonique de
désigne la base
canonique de
 R3, il est usuel d'exprimer un tenseur sous
sa forme matricielle dans la base canonique en chaque point de
Ω où il est défini :
R3, il est usuel d'exprimer un tenseur sous
sa forme matricielle dans la base canonique en chaque point de
Ω où il est défini :
 M
M =
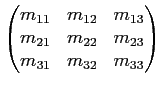
où chaque coefficient mij est une fonction scalaire défini sur
Ω. Il est alors commode d'exprimer le tenseur comme une
combinaison linéaire des applications linéaires canoniques, notées
sous la forme d'un produit tensoriel
dont la représentation matricielle est la matrice nulle partout sauf
le coefficient de la i-ème ligne j-ème colonne qui vaut 1.
Par exemple,
Ainsi, on écrit
choi
2008-12-22
![]() désigne la base
canonique de
désigne la base
canonique de
![]() R3, il est usuel d'exprimer un tenseur sous
sa forme matricielle dans la base canonique en chaque point de
Ω où il est défini :
R3, il est usuel d'exprimer un tenseur sous
sa forme matricielle dans la base canonique en chaque point de
Ω où il est défini :