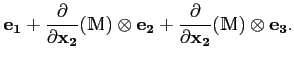suivant: Divergence d'un tenseur d'ordre monter: Calcul différentiel sur un précédent: Tenseur d'ordre 2 Table des matières Index
Par définition, la dérivée (ou le gradient) d'un tenseur en un point est un
élément de
![]() (
(![]() R3,
R3,![]() (
(![]() R3)). Or il
existe une bijection naturelle entre
R3)). Or il
existe une bijection naturelle entre
![]() (
(![]() R3,
R3,![]() (
(![]() R3)) et
R3)) et
![]() (
(![]() (
(![]() R3),
R3),![]() R3).
R3).
D'autre part, dans la base canonique (base fixe), on a naturellement