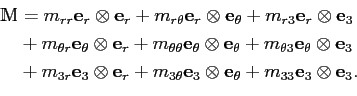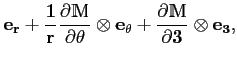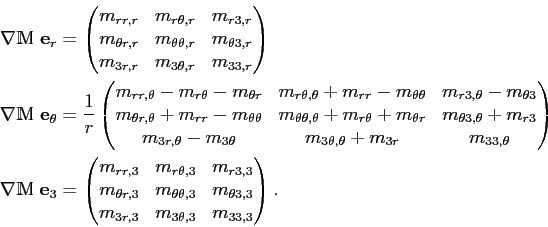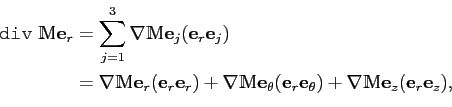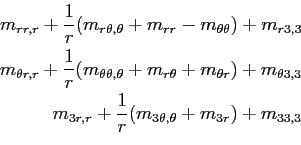Tenseur en coordonnées cylindriques

Soit $\mathbbm$M un tenseur d'ordre 2 définie sur une partie de $\mathbbm$R³, alors $\mathbbm$M se décompose en coordonnées cartésiennes :

$$\mathbbm$$M = $$\sum_{{i= 1}}^{{3}}$$$$\sum_{{j= 1}}^{{3}}$$m_ij$$\bf{e}{_{i}\otimes \vec{e}_{j}.$$

On a de même en coordonnées cylindriques

$$\begin{aligned}\mathbbm{M} &= m_{rr} \vec{e}_{r} \otimes \vec{e... ..._{\theta} + m_{33} \vec{e}_{3} \otimes \vec{e}_{3}. \end{aligned}$$

Or toutes les dérivées partielles sont nulles sauf

$$\begin{aligned}& \frac{\partial{}}{\partial{\theta}} (\vec{e}_{... ...artial{\theta}} = -\vec{e}_{3} \otimes \vec{e}_{r}. \end{aligned}$$

Mais le gradient est donné par

∇$$\mathbbm$$M   = $${\frac{{\partial{\mathbbm{M}}}}{{\partial{r}}}}$$⊗$$\bf{e}{_{r} + \frac{1}{r} \frac{\partial{\mathbbm{M}}}{\partial{... ...c{e}_{\theta} + \frac{\partial{\mathbbm{M}}}{\partial{3}} \otimes \vec{e}_{3},$$

d'où on tire l'expression du gradient de $\mathbbm$M en coordonnées cylindriques :

$$\begin{aligned}\nabla{\mathbbm{M}}\;&= m_{rr,r} \vec{e}_{r} \ot... ...vec{e}_{3} \otimes \vec{e}_{3} \otimes \vec{e}_{3}. \end{aligned}$$

C'est à dire, de façon légèrement plus lisible ;) :

$$\begin{aligned} \nabla{ \mathbbm{M}}\;\vec{e}_{r} &= \begin{p... ..._{3r,3} & m_{3\theta,3} & m_{33,3} \end{pmatrix} . \end{aligned}$$

La divergence d'un tenseur est définie comme précédemment :

$$\begin{aligned} \div{\mathbbm{M}}\vec{e}_{r} &=\sum_{j=1}^3\n... ... \nabla\mathbbm{M}\vec{e}_z(\vec{e}_r\vec{e}_z), \end{aligned}$$

de même, on a :

$$\begin{aligned} \div{\mathbbm{M}}\vec{e}_{\theta} &= \nabla\m... ...abla\mathbbm{M}\vec{e}_z(\vec{e}_\theta\vec{e}_z), \end{aligned}$$

et

$$\begin{aligned} \div{\mathbbm{M}}\vec{e}_{r} &= \nabla\mathbb... ...+ \nabla\mathbbm{M}\vec{e}_z(\vec{e}_z\vec{e}_z). \end{aligned}$$

On obtient donc finalement :

Proposition 7.4.1   La divergence d'un tenseur d'ordre 2 en coordonnées cylindrique

[div $$\mathbbm$$M]_cyl = $$\left(\vphantom{ \begin{aligned} m_{rr,r} + \frac{1}{r}(m_{r\th... ...,r} +\frac{1}{r}(m_{3\theta,\theta} +m_{3r} ) + m_{33,3} \end{aligned}}\right.$$$$\begin{aligned} m_{rr,r} + \frac{1}{r}(m_{r\theta,\theta}+m_{r... ...frac{1}{r}(m_{3\theta,\theta} +m_{3r} ) + m_{33,3} \end{aligned}$$$$\left.\vphantom{ \begin{aligned} m_{rr,r} + \frac{1}{r}(m_{r\th... ...,r} +\frac{1}{r}(m_{3\theta,\theta} +m_{3r} ) + m_{33,3} \end{aligned}}\right)$$.

Il peut être parfois avantageux de le récrire sous la forme suivante :

[div $$\mathbbm$$M]_cyl = $$\left(\vphantom{ \begin{aligned}& \frac{1}{r}\frac{\partial{}}{\... ...{\partial{}}{\partial{x_{3}}}(m_{33}) +\frac{1}{r} m_{3r} \end{aligned}}\right.$$$$\begin{aligned}& \frac{1}{r}\frac{\partial{}}{\partial{r}}(rm_{... ...ial{}}{\partial{x_{3}}}(m_{33}) +\frac{1}{r} m_{3r} \end{aligned}$$$$\left.\vphantom{ \begin{aligned}& \frac{1}{r}\frac{\partial{}}{\... ...{\partial{}}{\partial{x_{3}}}(m_{33}) +\frac{1}{r} m_{3r} \end{aligned}}\right)$$