Définition 9.1.1
On peut définir l'ensemble des nombres complexes par
 C
C = {(
a,
b)∈
 R2
R2 muni des somme et multiplication complexes}.
On pose i = (0, 1) et on note
z = (a, b) = a + ib, a désigne alors la partie réelle et b désigne la
partie imaginaire de z.
Définition 9.1.2
Les somme et multiplication complexes sont définies, pour z = a + ib et
z′ = a′ + ib′, par :
-
z + z′ = (a, b) + (a′, b′) = (a + a′, b + b′).
-
zz′ = (aa′ - bb′, ab′ + a′b).
Par exemple pour z = (0, 1) = i on a
z2 = zz = (0, 1)(0, 1) = (- 1, 0) = - 1.
Ainsi, à chaque point du plan de
 R2 on fait correspondre
un unique nombre complexe; C'est pourquoi on parle de plan complexe.
R2 on fait correspondre
un unique nombre complexe; C'est pourquoi on parle de plan complexe.
Figure 7.1:
Un nombre complexe
z = a + ib
|
|
Proposition 9.1.3
Pour tout nombre complexe z et
z′, on a
-
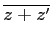 =
= 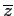 +
+ 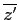
-
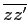 =
= 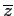
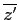
-
z +
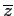 = 2Re(z) et
z -
= 2Re(z) et
z - 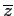 = 2iIm(z)
= 2iIm(z)
-
z
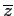 est réel et si z≠ 0,
z
est réel et si z≠ 0,
z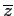 > 0
> 0
Définition 9.1.4
On appelle module de z le nombre réel positif
 z
z = (z
= (z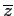 )1/2.
)1/2.
Proposition 9.1.5
Soit z un nombre complexe non nul alors
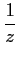
=
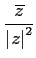
Proposition 9.1.6
Soit z un nombre complexe
-
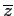
 =
=  z
z
-
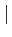 zz′
zz′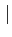 =
= 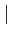 z
z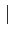
 z′
z′
-
 Re(z)
Re(z) ≤
≤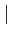 z
z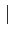 et
et
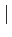 Im(z)
Im(z)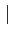 ≤
≤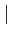 z
z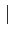
-
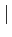 z+z′
z+z′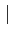 ≤
≤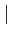 z
z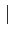 +
+ 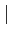 z′
z′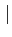
Proposition 9.1.7
Soient
a1,..., an et
b1,..., bn des nombres
complexes.
Nous terminons cette présentation par les propriétés principales de
 C :
C :
Théorème 9.1.8
L'ensemble des nombres complexes, avec ses addition et
multiplication complexes, possède une structure de corps. On parle
de corps des nombres complexes.
Théorème 9.1.9
Le corps des nombres complexes est algébriquement clos.
Autrement dit, les solutions de toute équation algébrique à
coefficients complexes sont encore des nombres complexes. Par exemple,
le corps des réels
 R n'est pas algébriquement clos puisque
l'équation
x2 + 1 = 0 ne possède pas de solutions réelles mais des
solutions complexes.
R n'est pas algébriquement clos puisque
l'équation
x2 + 1 = 0 ne possède pas de solutions réelles mais des
solutions complexes.
Théorème 9.1.10
Soit
P(z) = 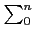 aizi un polynôme de degré n à
coefficients complexes. Alors P se factorise
aizi un polynôme de degré n à
coefficients complexes. Alors P se factorise
P(
z) =
an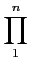
(
z -
ri)
où les ri sont les n racines de P (comptées avec leurs
multiplicités).
choi
2008-12-22
![]() R2 on fait correspondre
un unique nombre complexe; C'est pourquoi on parle de plan complexe.
R2 on fait correspondre
un unique nombre complexe; C'est pourquoi on parle de plan complexe.
![]() C :
C :