Sous-sections
Soit Ω une partie non vide du plan complexe
 C.
Considérons une fonction f à valeur complexe définie
sur Ω.
Soit
z0∈Ω⊂
C.
Considérons une fonction f à valeur complexe définie
sur Ω.
Soit
z0∈Ω⊂ C, on sait que
f est différentiable en z0, si il existe un nombre complexe,
noté
f′(z0) tel que :
C, on sait que
f est différentiable en z0, si il existe un nombre complexe,
noté
f′(z0) tel que :
f (z0 + h) = f (z0) + f′(z0)h + o(h).
Bien entendu si un tel nombre existe, il est égal à
f′(
z0) =
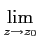
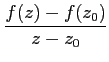
C'est la dérivée de f au point z0.
Pour
z = (x, y) = x + iy, introduisons les notations :
Définition 9.2.1
Si f est différentiable dans tout Ω, alors on
dit que f est holomorphe (ou analytique) dans Ω si
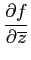
= 0 dans
Ω.
Par exemple, les fonctions analytiques sont évidemment holomorphes
dans leurs domaines de convergence, mais aussi la fonction
f (
z) =
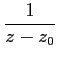
est holomorphe dans
 C - B(z0,
C - B(z0, ), ou même dans
), ou même dans
 C - {z0}.
C - {z0}.
Par contre la fonction
f (z) = 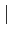 z
z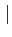 n'est pas holomorphe dans aucune
partie de
n'est pas holomorphe dans aucune
partie de
 C.
C.
On a les propriétés suivantes :
Proposition 9.2.2
Si f et g sont holomorphes dans Ω, alors
le sont aussi.
Proposition 9.2.3
Si f est holomorphe dans Ω et g est holomorphe dans
f (Ω), alors la fonction composée
(fog) est holomorphe
dans Ω et :
(fog)′ = g′(f (z0))f′(z0).
Théorème 9.2.4
Soit f une fonction complexe définie dans
Ω⊂ C,
on décompose f suivant sa partie réelle P et sa partie imaginaire
Q, avec
z = (x, y) = x + iy :
C,
on décompose f suivant sa partie réelle P et sa partie imaginaire
Q, avec
z = (x, y) = x + iy :
f (z) = P(x, y) + iQ(x, y).
f est une fonction holomorphe si et seulement si
P et Q satisfont aux conditions de Cauchy-Riemann :
Corollaire 9.2.5
Si
f = P + iQ est holomorphe, alors les fonctions réelles P et
Q sont nécessairement harmoniques.
Terminons par cette question que nous laissons au lecteur :
Existe-t-il une fonction définie sur une variable complexe qui soit
différentiable mais pas holomorphe ?
choi
2008-12-22
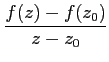
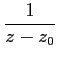
![]() z
z![]() n'est pas holomorphe dans aucune
partie de
n'est pas holomorphe dans aucune
partie de
![]() C.
C.