suivant: Espace des fonctions infiniment monter: Introduction à la théorie précédent: Introduction à la théorie Table des matières Index
C'est à Paris, en 1944, que Laurent Schwartz invente, en une nuit, sa théorie des distributions, théorie qui lui vaudra une médaille Fields en 1950. Comme il le décrit lui-même dans son autobiographie [Sch97], la théorie des distributions était inévitable, et plusieurs théories contemporaines en étaient très proches dont notamment la théorie de Sobolev.
La nécessité d'une théorie allant au delà de la définition classique des fonctions et du calcul différentiel s'imposait par des exemples:
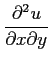 = 0
= 0
choi 2008-12-22