Définition 13.2.1
Le support d'une fonction continue f est la fermeture (ou l'adhérence) de l'ensemble des x tels que
f (x)≠ 0. On note :
supp f =
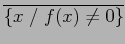
Proposition 13.2.2
Dans
 Rn les ensembles compacts sont les ensembles fermés bornés.
Rn les ensembles compacts sont les ensembles fermés bornés.
Définition 13.2.3
L'ensemble des fonctions infiniment dérivables à support compact dans
Ω⊂ Rn est noté
Rn est noté
 D(Ω).
D(Ω).
Exemples.
On munit
 D d'une pseudo-topologie :
D d'une pseudo-topologie :
Définition 13.2.4
On dit qu'une suite
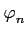 ∈
∈ D converge vers 0 si et seulement si ∃K un compact tel que
supp
D converge vers 0 si et seulement si ∃K un compact tel que
supp 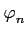 ∈K ∀n et :
∈K ∀n et :
On voit que les conditions de convergence sont ``sévères'' : on dit que c'est une topologie fine (exigeante).
choi
2008-12-22
![$\displaystyle \begin{array}[c]{ll}
e^{\frac{-1}{1 - \left\vert{x}\right\vert^2}} &\left\vert{x}\right\vert< 1\\
0 & \left\vert{x}\right\vert\geq 1
\end{array}$](img683.png)