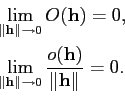Éléments de topologie métrique

Le titre de cette section est trompeur, il ne s'agit ici que de rappeler quelques définitions usuelles en topologie métrique, il n'y a aucune propriété énoncée. Il s'agit pour l'essentiel de donner un sens à la notion de convergence pour des objets autre que des scalaires...

Rappelons que dans $\mathbbm$Rⁿ, un ouvert O est une partie de $\mathbbm$Rⁿ telle que pour tout élément x₀ de O, la boule (fermée) de centre x₀ et de rayon $\varepsilon$ > 0,

B(x₀,$$\varepsilon$$) = {x∈$$\mathbbm$$Rⁿ, tel que $$\left\vert\vphantom{{x_{0}-x}}\right.$$x₀-x$$\left.\vphantom{{x_{0}-x}}\right\vert$$≤$$\varepsilon$$},

soit incluse dans O pour tout $\varepsilon$ suffisamment petit.

Par ailleurs un ensemble sera dit fermé si son ensemble complémentaire est ouvert. Autrement dit, une partie de $\mathbbm$Rⁿ est ouverte si elle ne contient aucun point de sa frontière, tandis qu'une partie de $\mathbbm$Rⁿ est fermée si elle contient tous les points de sa frontière. On remarquera, qu'au contraire d'une porte, un ensemble peut être ni ouvert ni fermé.

La raison pour laquelle le calcul différentiel se fait sur des ensembles ouverts est, disons, technique. Il s'agit pour l'essentiel d'éliminer des petites subtilités pouvant survenir sur le bord des ensembles considérés (par exemple la notion de continuité à gauche ou à droite dans le cas d'une fonction d'une variable réelle). Il n'y a donc pas lieu d'insister trop sur cet aspect de la théorie dans un premier temps.

Dans toute la suite, la norme d'un vecteur $\bf{x}{$ de $\mathbbm$Rⁿ est la norme euclidienne usuelle, si

$$\bf{x}{ = \sum_{i=1}^{n}x_{i}\vec{e}_{i}$$

les $\left\{\vphantom{\vec{e}_{i}}\right.$$\bf{e}{_{i}$$\left.\vphantom{\vec{e}_{i}}\right\}$ désignant la base canonique de $\mathbbm$Rⁿ, alors

|$$\bf{x}{$$| = $$\sqrt{{\sum_{i=1}^{n}(x_{i})^{2}}}$$.

Il est facile de vérifier que cette norme satisfait aux conditions définissant une norme :

$$\begin{aligned} &{\Vert{\vec{x} + \vec{y}}\Vert}_{} \leq {\Vert... ...t{ \vec{x}}\Vert}_{} = 0 \Leftrightarrow \vec{x}=0. \end{aligned}$$

Définition 4.1.1   On dira d'un élément (ou vecteur) $\bf{x}{$ de $\mathbbm$Rⁿ qu'il converge vers un autre élément $\bf{x}{_{0}$ de $\mathbbm$Rⁿ si la norme de la différence $\bf{x}{_{0} - \vec{x}$ tend vers 0 :

$$\bf{x}{ \longrightarrow \vec{x}_{0} \Leftrightarrow {\Vert{ \vec{x}_{0} - \vec{x}}\Vert}_{} \longrightarrow 0.$$

Définition 4.1.2   Une suite $\bf{x}{_{n}$ de $\mathbbm$Rⁿ est une suite de Cauchy si et seulement si

$$\lim_{{n,m\rightarrow +\infty}}^{}$$|$$\bf{x}{_{n}- \vec{x}_{m}$$| = 0.

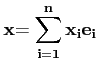
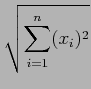Par ailleurs, on est amené à utiliser souvent la notion de reste négligeable, notés petit o et grand O dans le sens où

$$\begin{aligned} &\lim_{{\Vert{\vec{h}}\Vert}_{}\rightarrow 0} O... ... 0} \frac{o(\vec{h})}{{\Vert{\vec{h}}\Vert}_{}} =0. \end{aligned}$$

Remarque 4.1.3   Les notions de convergences et de suite de Cauchy, présentées ici, se généralisent sans modification à tout espace vectoriel de dimension finie ou non, muni d'une norme.