Proposition 5.3.1
soit f une fonction Riemann-intégrable et soit F la fonction définie par
F(
x) =
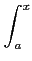 f
f (
t)
dt
Alors, F est une fonction continue et dérivable : on a de plus
F′(x) = f (x).
Théorème 5.3.2
Théorème fondamental -
Soit f une fonction Riemann-intégrable sur [a, b], si
F′(x) = f (x), alors
F(
b) -
F(
a) =
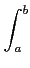 f
f (
x)
dx
Corollaire 5.3.3
Intégration par partie -
Soient u et v deux fonctions dérivables sur [a, b].
u(
b)
v(
b) -
u(
a)
v(
a) =
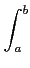 u′
u′(
x)
v(
x)
dx +
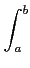 v′
v′(
x)
u(
x)
dx
choi
2008-12-22