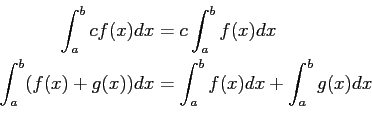Proposition 5.2.1
Si f et g sont Riemann-intégrables alors f + g l'est également.
Proposition 5.2.2
Si f et g sont Riemann-intégrables alors fg l'est également.
Proposition 5.2.3
Si
f (x)≤g(x) ∀x∈[a, b] alors
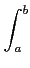 f
f (
x)
dx≤
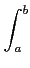 g
g(
x)
dx.
Proposition 5.2.4
Relation de Chasles - Si f est Riemann-intégrable sur
I⊂ R,
R,
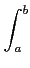 f
f (
x)
dx =
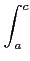 f
f (
x)
dx +
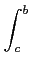 f
f (
x)
dx ∀
a,
b,
c∈
I
Proposition 5.2.5
Si f et g sont Riemann-intégrables sur [a, b] et que c est une constante, alors
On retiendra en particulier que l'opérateur intégrale est une forme
linéaire sur l'ensemble des fonctions Riemann-intégrables.
Proposition 5.2.6
Si
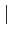 f
f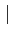 est Riemann-intégrable sur [a, b]
alors,
est Riemann-intégrable sur [a, b]
alors,
On retiendra tout particulièrement le résultat fondamental :
Théorème 5.2.7
Changement de variable - Soit f une fonction Riemann-intégrable sur
[a, b] et 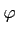 une fonction dérivable définie sur [A, B] et
telle que
une fonction dérivable définie sur [A, B] et
telle que
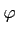 (A) = a et
(A) = a et
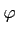 (B) = b
(B) = b
choi
2008-12-22