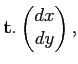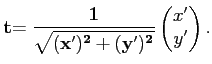Définition 6.1.1
Une k-surface Ω dans
 Rn, est l'image par un
difféomorphisme T d'un domaine
D∈
Rn, est l'image par un
difféomorphisme T d'un domaine
D∈ Rk à valeur dans
Rk à valeur dans
 Rn. On dit que la k-surface est de classe Cm, si
l'application T est de classe Cm.
Rn. On dit que la k-surface est de classe Cm, si
l'application T est de classe Cm.
On dit aussi que la k-surface
Ω∈ Rn est une
sous-variété de dimension k plongée dans
Rn est une
sous-variété de dimension k plongée dans
 Rn.
Rn.
Définition 6.1.2
On note
ω = 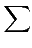 ai1,..., ikdxi1∧...∧dxik ai1,..., ikdxi1∧...∧dxik |
(6.1) |
une k-forme différentielle ou forme différentielle d'ordre k, la
forme linéaire qui à toute k-surface
Ω∈ Rn de
classe C1, image par T de
D∈
Rn de
classe C1, image par T de
D∈ Rk, fait
correspondre la quantité :
Rk, fait
correspondre la quantité :
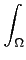 ω
ω =
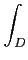
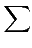 ai1,..., ik
ai1,..., ik(
T(
u))
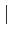 JT
JT(
u)
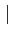 du
du
où
désigne le Jacobien de l'application
(u1,..., uk)→(Ti1(u),..., Tik(u)).
Remarque 6.1.3
Convention: une forme différentielle d'ordre 0 est une fonction.
Remarque 6.1.4
La notation (4.1) est unique si les xij sont numérotés
et pris dans un ordre croissants.
On remarque que cette définition reprend simplement la formule de
Jacobi de changement de variable dans les intégrale multiples, si bien
que cette définition est indépendante du choix de D et de T.
Cette définition permet de généraliser la notion d'intégrale sur une
courbe définie dans la section précédente. En effet, considérons un
contour γ de
 R2 défini par
R2 défini par
γ = {(
x,
y)∈
 R2
R2 (
x,
y) = (
x(
t),
y(
t)) =
T(
t)
t∈[
a,
b]}.
Et posons
ω =
f (
x,
y)
ds avec
ds =
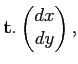
où 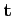 est la tangente unitaire à γ, on peut prendre
est la tangente unitaire à γ, on peut prendre
Alors, ω est la forme linéaire qui fait correspondre à γ
l'intégrale de f sur γ:
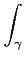 ω
ω =
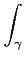 f
f (
x,
y)
ds =
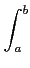 f
f (
x(
t),
y(
t))
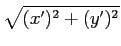 dt
dt
Proposition 6.1.5
Dans
 Rn une n + 1 forme différentielle est une forme nulle.
Rn une n + 1 forme différentielle est une forme nulle.
choi
2008-12-22
![]() Rn est une
sous-variété de dimension k plongée dans
Rn est une
sous-variété de dimension k plongée dans
![]() Rn.
Rn.
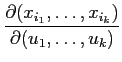
![]() R2 défini par
R2 défini par