La notation
ω =
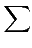 ai1,..., ikdxi1
ai1,..., ikdxi1∧...∧
dxik
d'une forme différentielle provient de la
définition du produit de deux formes différentielles :
Définition 6.2.1
Le produit extérieur des deux 1-formes différentielles dx et dy
est la 2-forme différentielle
dx∧dy. Elle est
notée avec le symbole ∧.
Proposition 6.2.2
dx∧dy = - dy∧dx.
On généralise alors
Définition 6.2.3
Produit extérieur - On définit le produit extérieur de deux formes
différentielles
ω1 et
ω2 par les règles de calcul
:
-
ω1∧ω2 = - ω2∧ω1
-
ω1∧(ω2 + ω3) = ω1∧ω2 + ω1∧ω3
Par exemple
(fdx∧dz)∧(gdx + hdy) = - hfdx∧dy∧dz.
Théorème 6.2.4
Il existe un opérateur nommé différentielle et noté d
qui à toute k - 1 forme différentielle ω fait correspondre une
k-forme différentielle dω avec les règles suivantes :
-
d (dω) = 0
-
df (x1,..., xn) = ∂x1fdx1 + ... + ∂xnfdxn
-
d
 f (x1,..., xn)dxi1∧...∧)dxik
f (x1,..., xn)dxi1∧...∧)dxik = df (x1,..., xn)∧
= df (x1,..., xn)∧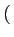 dxi1∧...∧)dxik
dxi1∧...∧)dxik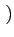
Ainsi, le produit d'une k1-forme et d'une k2 forme
différentielle donne une
(k1 + k2)-forme différentielle.
choi
2008-12-22