Considérons la série
f (
z) =
 anzn
anzn
où
z∈ C et
an∈
C et
an∈ C.
On définit le rayon de
convergence R de la série f (z) par :
C.
On définit le rayon de
convergence R de la série f (z) par :
 |
= 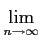 sup sup an an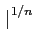 (règle de Cauchy) (règle de Cauchy) |
|
| |
= 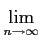 sup sup 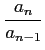  (règle de d'Alembert). (règle de d'Alembert). |
|
C'est à dire que la série diverge si
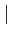 z
z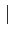 > R et elle converge si
> R et elle converge si
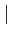 z
z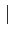 < R. Le cas
< R. Le cas
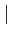 z
z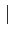 = R étant sujet à discussion.
= R étant sujet à discussion.
Par ailleurs, cette convergence est normale et donc uniforme dans tout
disque centré de rayon
R′ < R. Alors, d'après les théorèmes
d'inversion des limites vus en premier cycle, on a
Proposition 9.3.1
∀z,
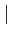 z
z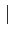 < R, la fonction d'une variable complexe f (z)
est continue, infiniment
< R, la fonction d'une variable complexe f (z)
est continue, infiniment
 C-dérivable, les dérivées
s'obtenant en dérivant dans chaque terme de la série :
C-dérivable, les dérivées
s'obtenant en dérivant dans chaque terme de la série :
f(k)(
z) =

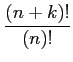 an+kzn
an+kzn
On dit que f (z) est analytique dans
{z∈ C/
C/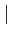 z
z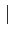 < R}. Si f (z) est analytique dans
< R}. Si f (z) est analytique dans
 C, on dit que
f est entière.
C, on dit que
f est entière.
choi
2008-12-22
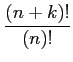 an+kzn
an+kzn