Sous-sections
Commençons par des valeurs remarquables (obtenues facilement en
appliquant le théorème de Fubini au carré des intégrales recherchées):
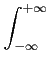 e-x2dx e-x2dx |
= |
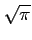 . . |
(12.1) |
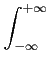 e- e-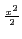 dx dx |
= |
 . . |
(12.2) |
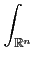 e- e-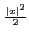 dx dx |
= |
(2π)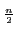 . . |
(12.3) |
Espace
 S(
S(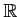 n)
n)
Définition 12.1.1
 S(
S(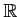 n) est l'ensemble des fonctions
f∈
n) est l'ensemble des fonctions
f∈ C∞(
C∞(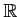 n) telles que
∀α∈
n) telles que
∀α∈ Nn,
∀k∈
Nn,
∀k∈ N
N
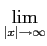
|
x|
k|
Dαf (
x)| = 0
où on note
| x| = 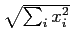 ,
α = (α1,..., αn) et
,
α = (α1,..., αn) et
Dαf (
x) =

On appelle
 S(
S( n) l'ensemble des fonctions à décroissance rapide sur
n) l'ensemble des fonctions à décroissance rapide sur
 n. On l'appelle également espace de Schwarz. C'est un espace
vectoriel.
n. On l'appelle également espace de Schwarz. C'est un espace
vectoriel.
Exemples.
-
 D(
D( n)⊂
n)⊂ S, noté également par
S, noté également par
 C∞0(
C∞0( n).
n).
-
e-x2∈
 S(
S(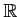 ).
).
- e-| x| n'est pas dans
 S (non différentiable en
0).
S (non différentiable en
0).
Nous avons les définitions équivalentes :
Proposition 12.1.2
 S est l'ensemble des fonctions f définies sur
S est l'ensemble des fonctions f définies sur
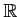 n telles
que
n telles
que
-
∀α,
∀β,
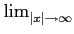 | xβ∂αf (x)| = 0 (si β = (β1,..., βn) on posexβ = x1β1 ... xnβn).
| xβ∂αf (x)| = 0 (si β = (β1,..., βn) on posexβ = x1β1 ... xnβn).
-
∀α, ∀k,
| x|k|∂αf (x)| soit bornée.
-
∀α,
∀β,
| xβ∂αf (x)| soit bornée.
-
∀α, ∀k,
| x|k|∂αf (x)| soit Lebesgue-intégrable.
-
∀α,
∀β,
| xβ∂αf (x)| soit intégrable.
Théorème 12.1.3
 S est dense dans
S est dense dans
 L1 et dans
L1 et dans
 L2.
L2.
Voir les suites régularisantes.
Soit f et g deux fonctions de
 L1(
L1( Rn), alors
Le produit de convolution de f et g est la fonction
Rn), alors
Le produit de convolution de f et g est la fonction
f*
g(
x) =
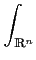 f
f (
x -
y)
g(
y)
dy.
Les principales propiétés du produit de convolution sont :
- Le produit est commutatif
- L'effet de régularisation : si
Dαf est définie et appartient à
 L1(
L1( Rn), alors
Rn), alors
Dα(f*g)(x) = Dαf*g(x)
Soit la fonction ρ de classe
C∞ à support compact :
ρ(
x) =
![$\displaystyle \left\{\vphantom{
\begin{array}[l]{ll}
e^{\frac{-1}{1-\left\vert{...
...{x}\right\vert\leq 1\\
0 & \left\vert{x}\right\vert\geq 1
\end{array}}\right.$](img653.png)
![$\displaystyle \begin{array}[l]{ll}
e^{\frac{-1}{1-\left\vert{x}\right\vert^2}} ...
...eft\vert{x}\right\vert\leq 1\\
0 & \left\vert{x}\right\vert\geq 1
\end{array}$](img654.png)
Alors la suite
ρm(x) = ρ(mx) est une suite régularisante au
sens que si
f∈ L1(
L1( Rn) (resp.
Rn) (resp.
 L2)
alors,
fm = f*ρm est dans
L2)
alors,
fm = f*ρm est dans 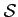 est converge vers f dans
est converge vers f dans
 L1 (resp. dans
L1 (resp. dans
 L2).
choi
2008-12-22
L2).
choi
2008-12-22

![$\displaystyle \begin{array}[l]{ll}
e^{\frac{-1}{1-\left\vert{x}\right\vert^2}} ...
...eft\vert{x}\right\vert\leq 1\\
0 & \left\vert{x}\right\vert\geq 1
\end{array}$](img654.png)