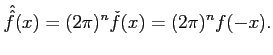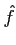 , notée aussi
, notée aussi
 Ff, s'appelle la transformée de
Fourier de f. Elle existe car
| e-ix.yf (x)| < | f (x)| et
f∈
Ff, s'appelle la transformée de
Fourier de f. Elle existe car
| e-ix.yf (x)| < | f (x)| et
f∈ L1.
L1.
Théorème 12.2.2
Soit
f∈ L1, sa transformée de Fourier
L1, sa transformée de Fourier
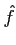 est continue, bornée et tend vers 0 a l'infini.
est continue, bornée et tend vers 0 a l'infini.
Remarque 12.2.3
Pour une fonction f quelconque dans
 L1,
L1, 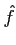 n'est pas
nécessairement dans
n'est pas
nécessairement dans
 L1
L1
Lemme 12.2.4
La transformation de Fourier est ``invariante``
pour
f (x) = e-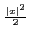 :
:
Théorème 12.2.5
Pour toute fonction
f∈ S et
S et
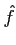 ∈
∈ S et nous
avons les relations:
S et nous
avons les relations:
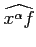 |
= |
(i)| α|∂α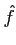 (y) (y) |
(12.5) |
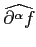 |
= |
(iy)α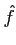 |
(12.6) |
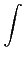 ψ(y) ψ(y)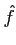 (y)dy (y)dy |
= |
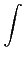 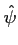 (y)f (y)dy (y)f (y)dy |
(12.7) |
La transformation de Fourier a donc la propriété fondamentale
d'échanger les multiplications et les dérivations. Les propriétés précédentes
restent valables tant qu'elles ont un sens.
Nous avons le formule d'inversion :
Théorème 12.2.6
Si
f∈ L1 et
L1 et
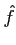 ∈
∈ L1, alors
L1, alors
f (
x) = (2
π)
-n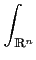 eix.y
eix.y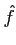
(
y)
dy
Remarque 12.2.7
si
f∈ L1 et
L1 et
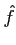 ∈
∈ L1 ,
L1 ,
Corollaire 12.2.8
Formule de Parseval -
Si
θ∈ S,
ψ∈
S,
ψ∈ L1,
L1,
Corollaire 12.2.9
Formule de Plancherel - si
ψ∈ S, alors
S, alors
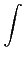
|
ψ|
2 = (2
π)
-n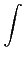
|
ψ|
2
Théorème 12.2.10
Si
f∈ L1 et
L1 et 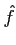 = 0, alors f = 0.
= 0, alors f = 0.
Autrement dit La transformation de Fourier est une application injective dans
 L1.
L1.
[on pourra par exemple prendre les (fν) dans
 D(
D( n), ou même la suite régularisée par convolution].
n), ou même la suite régularisée par convolution].
Remarque 12.2.12
Pour
f∈ L2, on n'a pas
L2, on n'a pas
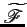 f (y) =
f (y) = 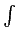 e-ix.yf (x)dx, en général.
e-ix.yf (x)dx, en général.
Proposition 12.2.13
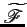 est bijective de
est bijective de
 L2 sur
L2 sur
 L2.
L2.
Par suite, on note abusivement, pour toute fonctions de
 L2,
L2,
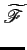
=
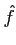
.
Théorème 12.2.14
La transformation de Fourier est un automorphisme topologique
de
 S.
S.
choi
2008-12-22