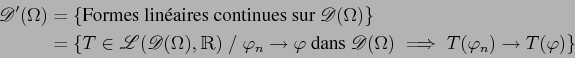Sous-sections
Définition 13.3.1
On note
 D′(Ω) le dual topologique de
D′(Ω) le dual topologique de
 D(Ω). On l'appelle l'espace des distributions sur Ω.
D(Ω). On l'appelle l'espace des distributions sur Ω.
On note indifféremment
T(
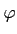
) = 〈
T,
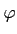
〉.
On définit l'ensemble
 L1loc des fonctions mesurables localement intégrable :
L1loc des fonctions mesurables localement intégrable :
 L1loc
L1loc =
 f
f /
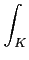 f
f < + ∞, ∀
K compact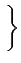
.
Proposition 13.3.2
 L1loc contient
L1loc contient
 L1,
L1,
 L2,
L2,
 Cm, ....
Cm, ....
Proposition 13.3.3
A toute fonction f de
 L1loc est associée une distribution qu'on notera dans un premier temps [f] :
L1loc est associée une distribution qu'on notera dans un premier temps [f] :
〈[
f],
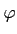
〉 =
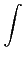
 Rnf
Rnf (
x)
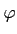
(
x)
dx ∀
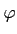
∈
 D
D.
Les distributions apparaissent ainsi comme une généralisation des fonctions.
Proposition 13.3.4
On note δ la distribution de Dirac, définie par
Définition 13.3.5
Soit T une distribution dans
Ω⊂ Rn, sa dérivée partielle par rapport à la variable xi est, par définition, la distribution
Rn, sa dérivée partielle par rapport à la variable xi est, par définition, la distribution
De même, on a pour tout multi-indice α :
〈
DαT,
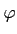
〉 = (- 1)
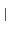 α
α
〈
T,
Dα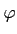
〉 ∀
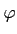
∈
 D
D
Ainsi, toute distribution est infiniment dérivable.
Par ailleurs, cette définition est une extension de la notion classique de dérivée :
Proposition 13.3.6
Soit
f∈ L1loc et supposons que sa dérivée
Dαf existe et soit localement intégrable, alors
[Dαf] (distribution associée à la dérivée) coïncide avec
Dα[f] (dérivée de la distribution associée).
L1loc et supposons que sa dérivée
Dαf existe et soit localement intégrable, alors
[Dαf] (distribution associée à la dérivée) coïncide avec
Dα[f] (dérivée de la distribution associée).
Proposition 13.3.7
Soit H(x) la fonction de Heaviside, alors
[H(x)]′ = δ0. Autrement dit, la dérivée de la fonction de Heaviside est la distribution de Dirac en 0.
Remarque 13.3.9
Si
T∈ D′(Ω) et
U∈
D′(Ω) et
U∈ D′(Ω), le produit n'est pas défini a priori.
D′(Ω), le produit n'est pas défini a priori.
Définition 13.3.10
- Translatée d'une distribution - Soit
T∈ D′(
D′( Rn) et
a∈
Rn) et
a∈ Rn, la translatée de T par a est la distribution
Rn, la translatée de T par a est la distribution
Définition 13.3.11
On dit qu'une suite de distribution Tn converge vers T au sens des distributions, si et seulement si
Définition 13.3.12
On note
supp T le support de la distribution
T∈ D′(Ω) défini par
D′(Ω) défini par
Exemples.
supp δ0 = {0}.
Proposition 13.3.13
Si une distribution est définie par une fonction f, on a
supp [f]⊂supp f.
Proposition 13.3.14
Si
supp T = {0} alors T est une combinaison linéaire de
distributions de Dirac en 0 et de ses dérivées.
T =
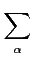 Cαδ0
Cαδ0.
choi
2008-12-22