Définition 13.5.1
Soit
T∈ D′ une distribution et
D′ une distribution et
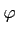 ∈
∈ D, le produit de convolution est la fonction défini par
D, le produit de convolution est la fonction défini par
T*
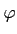
(
x) = 〈
Ty,
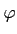 x
x-
y〉.
Exemples.
-
δ0*
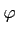 (x) =
(x) = 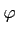 (x).
(x).
- si
f∈
 L1loc, alors
[f]*
L1loc, alors
[f]*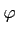 (x) = f*
(x) = f*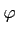 (x).
(x).
Proposition 13.5.2
Si
T∈ D′ et si
D′ et si
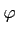 ∈
∈ D alors
T*
D alors
T*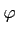 (x) est une fonction
(x) est une fonction
 C∞. De plus, on a
C∞. De plus, on a
∂
α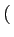 T
T*
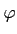
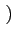
(
x) = ∂
αT*
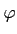
(
x) =
T*∂
α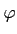
(
x).
Proposition 13.5.3
Si
T∈ E′ et si
E′ et si
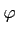 ∈
∈ D,
T*
D,
T*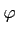 (x) est une fonction à support compact.
(x) est une fonction à support compact.
Théorème 13.5.4
 C∞ est séquentiellement dense dans
C∞ est séquentiellement dense dans
 D′.
D′.
Preuve : par le produit de convolution avec la suite régularisante.
Théorème 13.5.5
Si
T∈ D′ et
T′ = 0, alors T est une constante.
D′ et
T′ = 0, alors T est une constante.
choi
2008-12-22