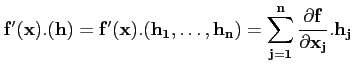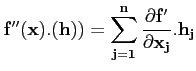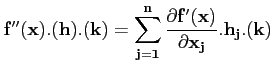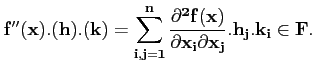Dérivée seconde
Soit  une application d'un ouvert
une application d'un ouvert
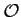 ⊂E vers
F où comme précédemment E et F désignent respectivement
⊂E vers
F où comme précédemment E et F désignent respectivement
 Rn et
Rn et
 Rm (ou encore tout espaces de Banach).
Rm (ou encore tout espaces de Banach).
On a vu que la différentielle (ou application dérivée) de  en
un point
en
un point  de
de 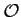 est une application linéaire de E
vers F :
est une application linéaire de E
vers F :
Ainsi,
en réapplicant la définition de différentielle à
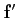 ,
on a :
,
on a :
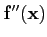 apparaît donc comme une application bilinéaire.
apparaît donc comme une application bilinéaire.
Puisque
E =  Rn,
Rn,
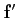 se décompose en
dérivées partielles :
se décompose en
dérivées partielles :
Il en est de même pour l'application dérivée seconde :
Ainsi,
et finalement
Théorème 4.7.1
Si  une application d'un ouvert
une application d'un ouvert
 ⊂E vers F est une application deux fois
différentiable en
⊂E vers F est une application deux fois
différentiable en  alors la
dérivée seconde est une application bilinéaire symétrique:
alors la
dérivée seconde est une application bilinéaire symétrique:
∀
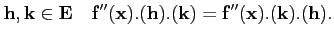
C'est un résultat non-trivial (excellent exercice en calcul
différentiel) mais qui donne immédiatement le
Corollaire 4.7.2
Théorème de Schwarz - Si  une application d'un ouvert
une application d'un ouvert
 ⊂E vers F est une application deux fois
différentiable en
⊂E vers F est une application deux fois
différentiable en  alors
alors

=
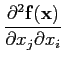
.
Ces résultats s'étendent à toutes les dérivées successives.
choi
2008-12-22
![]() en
un point
en
un point ![]() de
de ![]() est une application linéaire de E
vers F :
est une application linéaire de E
vers F :
![]() Rn,
Rn,
![]() se décompose en
dérivées partielles :
se décompose en
dérivées partielles :