Dans cette section, on énonce divers résultats théoriques
fondamentaux en calcul différentiel. Cependant ces résultats ne sont
pas nécessaire au niveau de la Licence de Mécanique.
Définition 4.8.1
On dit qu'un application différentiable 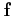 d'un ouvert
d'un ouvert 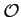 un ouvert de
un ouvert de
 Rn vers
Rn vers
 Rm est continûment
différentiable sur
Rm est continûment
différentiable sur 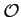 si
si
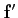 est une
application continue de
est une
application continue de 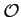 vers
vers
 (
( Rn,
Rn, Rm). On dit alors que
Rm). On dit alors que 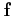 est de
classe
est de
classe
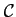 1, ce qu'on écrit
1, ce qu'on écrit
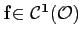 .
.
Théorème 4.8.2
Soit 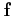 une application d'un ouvert
une application d'un ouvert 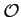 de
de
 Rn vers
Rn vers
 Rm. Alors
Rm. Alors
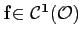 si et seulement si toutes les dérivées
partielles existent et sont continues sur
si et seulement si toutes les dérivées
partielles existent et sont continues sur 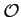 .
.
Théorème 4.8.3
Théorème de la Moyenne - Soit f une fonction continue et dérivable sur un intervalle [a, b]. Si la fonction dérivée
f′ est continue, alors il existe
c∈[a, b] telle que
f (b) - f (a) = (b - a)f′(c).
Lemme 4.8.4
Théorème du point fixe - Soit 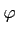 une application de E dans F, deux espaces de Banach. Si
une application de E dans F, deux espaces de Banach. Si 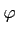 est contractante, alors
est contractante, alors 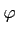 possède un unique point fixe.
possède un unique point fixe.
Cette partie est à compléter
choi
2008-12-22