suivant: Calcul différentiel sur un monter: Théorème de Stokes et précédent: Théorème de Stokes - Table des matières Index
Soit ω une 1-forme différentielle définie sur
![]() R2
par deux fonctions scalaire u1 et u2 définies sur
Ω⊂
R2
par deux fonctions scalaire u1 et u2 définies sur
Ω⊂![]() R2 :
R2 :
![\begin{equation*}\begin{aligned}
\int_{\Omega}(\frac{\partial{u_{1}}}{\partial{...
...2} \right)ds\\
&=\int_{[a,b]} \vec{u}.\vec{n} ds.
\end{aligned}\end{equation*}](img431.png)

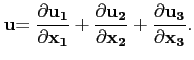
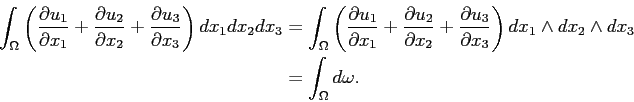
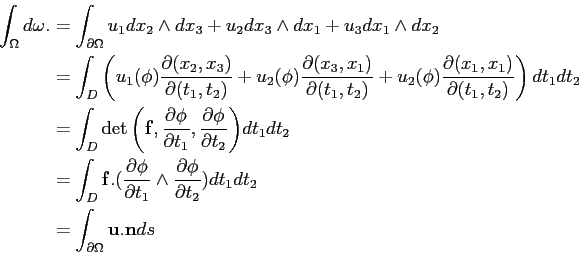
On admettra de façon plus générale le
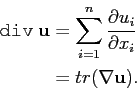
On étends la notion d'opérateur divergence aux champs de tenseur d'ordre 2 :
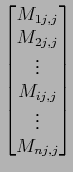
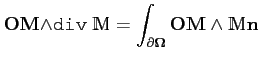
En appliquant la formule de de la divergence à
div ![]() M
M![]() où
où
![]() M est un tenseur d'ordre 2 défini dur un domaine Ω de
M est un tenseur d'ordre 2 défini dur un domaine Ω de
![]() R3 et
R3 et ![]() un champ de vecteur de
un champ de vecteur de ![]() également défini du Ω.
également défini du Ω.
On a alors
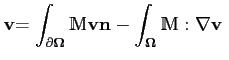

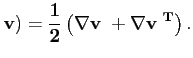
choi 2008-12-22