Sous-sections
Soit Ω un ouvert du plan complexe et soit γ(t) une
courbe dans Ω, pour t∈[a, b]. On décompose
γ(t) = x(t) + iy(t)
Soit
ω = f (z)dz une forme différentielle, où f est une fonction
de variable complexe définie sur ω à valeur dans
 C,
par définition on a
C,
par définition on a
Définition 9.5.1
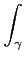 ω
ω =
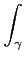 f
f (
z)
dz =
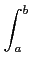 foγ
foγ(
t)
γ′(
t)
dt
où
γ([a, b]) = γ et
γ′(t) = x′(t) + iy′(t).
On a la propriété fondamentale :
Théorème 9.5.2
Soit f une fonction d'une variable complexe z si f est
dérivable dans Ω alors on a
On en déduit immédiatement
Corollaire 9.5.3
Formule intégrale de Cauchy - Si f est holomorphe dans Ω, un
domaine convexe de
 C alors
C alors
De plus on voit que f est infiniment dérivable avec
Théorème 9.5.4
Si f est holomorphe dans Ω alors pour tout chemin fermé γ dans
Ω, on a
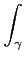 f
f (
z)
dz = 0
On dit que
φ(s) = 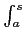 foγ(t)γ′(t)dt est une primitive de f le long de γ.
foγ(t)γ′(t)dt est une primitive de f le long de γ.
Corollaire 9.5.5
Si f est holomorphe sur Ω, alors f est de classe
C∞ sur Ω.
Théorème 9.5.6
Si f est holomorphe dans Ω, alors f se décompose en
série entière:
f (
ζ) =
 an
an(
ζ -
z0)
n ∀
z∈
Ω et ζ∈
V(
z0).
avec
Corollaire 9.5.7
Une fonction à variable complexe est holomorphe dans Ω si et seulement si elle est analytique dans Ω.
On termine par quelques résultats hors programmes mais néanmoins
importants
Théorème 9.5.8
Si une fonction est holomorphe et non constante alors elle
est ouverte
Corollaire 9.5.9
- Principe du maximum - Si f est
une fonction holomorphe dans un ouvert complexe Ω, et si
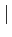 f
f atteint son maximum à l'intérieur de Ω, alors f est
une fonction constante sur Ω.
atteint son maximum à l'intérieur de Ω, alors f est
une fonction constante sur Ω.
Théorème 9.5.10
Soit f une fonction holomorphe non nulle dans un ouvert complexe
Ω, les zéros de f sont isolés.
En particulier si deux fonctions holomorphes ont des valeurs en un
nombre infini de points dans un domaine borné, alors les deux
fonctions sont identiques.
Soit f une fonction holomorphe sur une couronne
a < 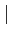 z-z0
z-z0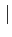 < b, d'après la formule de Cauchy,
< b, d'après la formule de Cauchy,
or
où la série est convergente si
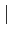 z
z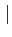 <
< 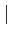 u
u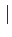 ou encore
ou encore
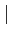 z-z0
z-z0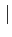 <
< 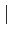 u-z0
u-z0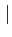 .
.
D'autre part, on a de même
où la série est convergente si
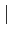 z
z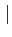 >
> 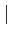 u
u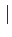 ou encore
ou encore
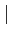 z-z0
z-z0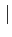 >
> 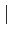 u-z0
u-z0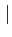 .
.
Par conséquent, en remplaçant (u - z) par
(u - z0) - (z - z0), on obtient
f (
z) =
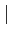
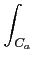 f
f (
u)

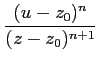 du
du +
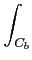 f
f (
u)

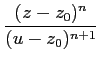 du
du![$\displaystyle \left.\vphantom{
\int_{C_{a}}f(u)\sum_{n=0}^{\infty}\frac{(u-z_{0...
...{C_{b}}f(u)\sum_{n=0}^{\infty}\frac{(z-z_{0})^{n}}{(u-z_{0})^{n+1}}du
}\right]$](img580.png)
Ainsi, on a montré le
Théorème 9.5.11
Soit f une fonction holomorphe sur une couronne
a < 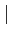 z-z0
z-z0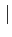 < b, il existe un développement unique de f :
< b, il existe un développement unique de f :
f (
z) =
 an
an(
z -
z0)
n
avec
C'est le développement de f en série de Laurent dans la couronne
a < 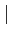 z-z0
z-z0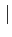 < b.
< b.
La notion de série de Laurent permet de définir la notion de Résidu :
Définition 9.5.12
Soit f une fonction holomorphe dans Ω sauf en des points
isolés (c'est toujours le cas). Le résidu de f en
zi∈Ω est la valeur complexe
Rés(
f,
zi) =
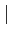
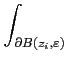 f
f (
z)
dz,
 suffisamment petit, de sorte que f est holomorphe dans
B(zi,
suffisamment petit, de sorte que f est holomorphe dans
B(zi, )
) 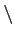 {zi}.
{zi}.
C'est aussi le coefficient a-1 du développement en série de
Laurent de f autour de zi.
Soit f une fonction holomorphe dans Ω sauf en un nombre fini
de points isolés
{z1,..., zm} Soit
 suffisamment petit pour que f soit holomorphe dans
Ω
suffisamment petit pour que f soit holomorphe dans
Ω 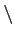
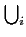 B(zi,
B(zi, ). Alors d'après le théorème
7.5.4, on a
). Alors d'après le théorème
7.5.4, on a
Autrement dit nous avons le
Théorème 9.5.13
- Théorème des Résidus - Soit f une fonction holomorphe dans
Ω sauf en un nombre fini de points isolés
{z1,..., zm}, alors
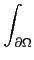 f
f (
z)
dz = 2
iπ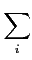
Rés(
f,
zi).
Pour faciliter le calcul d'un résidu, une classification est utile et
permet de s'affranchir de la détermination du développement en série
de Laurent.
Soit a un point de Ω qui apparaît comme un point singulier
d'une fonction f, c'est à dire que f n'est pas holomorphe a priori
en a. On classe ces pôles ou singularités suivant la possibilité de
prolonger
f (z)(z - a)k en une fonction holomorphe au voisinage de
a:
- Singularité ou Pôle illusoire : Si f est prolongeable par
continuité en a. Cela signifie que f est holomorphe en a, si
bien que
Rés(f, a) = 0.
On parle de pôle d'ordre 0.
- Singularité ou Pôle d'ordre k : Si
(z - a)kf (z) est
prolongeable par continuité en a mais pas
(z - a)k-1f (z). Le
résidu est alors obtenu par la formule intégrale de Cauchy :
Rés(
f,
a) =
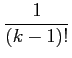
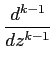
(
z -
a)
kf (
z)
![$\displaystyle \left.\vphantom{(z-a)^{k}f(z)}\right]_{{\vert _{z=a}}}^{}$](img592.png)
.
- Singularité essentielle : pour tout
k∈
 N
(z - a)kf (z) n'est pas prolongeable par continuité, on a pas le
choix, il faut trouver le développement en série de Laurent.
N
(z - a)kf (z) n'est pas prolongeable par continuité, on a pas le
choix, il faut trouver le développement en série de Laurent.
- Singularité à l'infini : si a est un point à l'infini on pose :
Rés(f (z),∞) = Rés(f (1/z), 0)
Théorème 9.5.14
Soit f une fonction holomorphe sauf en des points isolés.
Alors la somme des résidus, résidu à l'infini compris est nulle.
Nous terminons par un résultat très utile en calcul des résidus:
Proposition 9.5.15
Soit a une singularité d'ordre 1 d'une fonction f. Si f
s'exprime comme la fraction rationnelle irréductible de deux fonctions
holomorphe,
f (
z) =
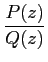
,
alors
Rés(
f,
a) =
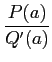
.
Une fonction holomorphe est une application conforme dans le sens où
elle laisse les angles inchangés en valeur et en sens.
choi
2008-12-22
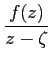 dz +
dz + 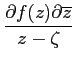 dz∧d
dz∧d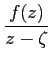 dz ∀ζ∈Ω.
dz ∀ζ∈Ω.
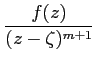 dz ∀ζ∈Ω.
dz ∀ζ∈Ω.
![]() foγ(t)γ′(t)dt est une primitive de f le long de γ.
foγ(t)γ′(t)dt est une primitive de f le long de γ.
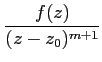 dz.
dz.
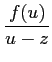 du +
du + 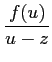 du
du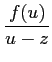 =
= 
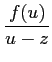 =
= 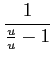
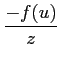
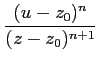 du +
du + 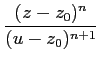 du
du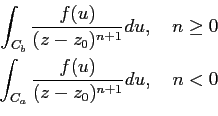
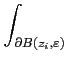 f (z)dz,
f (z)dz,
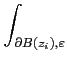 f (z)dz = 0.
f (z)dz = 0.
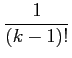
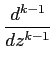
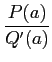 .
.