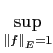Espace de Banach

Définition 14.1.1   Soit E un espace vectoriel normé, on dit que c'est un espace de Banach s'il est complet.

Autrement dit, E est complet si toute suite de Cauchy dans E est convergente.

La notion d'espace complet induit des résultats d'existence. C'est la raison essentielle pour laquelle on fait tant d'effort pour travailler dans des espaces de fonctions ayant cette propriété.

Quelques caractérisations abstraites d'un espace de Banach

Théorème 14.1.2   Soit E un espace vectoriel normé, alors E est complet si et seulement si les séries absolument convergentes (resp. normalement) sont convergentes.

Théorème 14.1.3   Soit E une espace vectoriel normé complet et soit un sous espace vectoriel F⊂E. Si F est fermé dans E, alors F est lui même complet pour la norme induite.

Théorème 14.1.4   Soit E un espace de Banach, alors son dual topologique E^′, c'est à dire l'ensemble des formes linéaires continues sur E est aussi un Banach pour la norme

| A|_E^′ = $$\sup_{{{\Vert{f}\Vert}_{E}=1}}^{}$$$$\left\vert\vphantom{{A(f)}}\right.$$A(f )$$\left.\vphantom{{A(f)}}\right\vert$$

Les espaces de Banach permettent de définir simplement la notion de fonction continue et par suite le notion de différentielle :

Définition 14.1.5   Soit E et F deux espaces de Banach réel, et soit f une fonction définie d'une partie ouverte U⊂E dans F. Alors f est continue en x∈U si et seulement si f (x + h) converge vers f (x) dans F, lorsque h converge vers 0 dans E :

f (x + h) = f (x) + O(h)

Définition 14.1.6   Soit E et F deux espaces de Banach réel, et soit f une fonction définie d'une partie ouverte U⊂E dans F. Alors f est différentiable en x∈U si et seulement si il existe une application linéaire A de E dans F (on note A∈$\cal {L}$(E, F)) telle que

f (x + h) = f (x) + Ah + o(h)

A est la dérivée de f en x, on la note généralement f^′(x).

Quelques exemples d'espaces de Banach

• Tout espace vectoriel réel ou complexe de dimension finie est un espace complet pour n'importe quelle norme.
• $\mathbbm$L¹(Ω) est complet pour tout Ω mesurable avec la norme
  | f|_{$\mathbbm$L¹(Ω)} = $$\int_{{\Omega}}^{}$$$$\left\vert\vphantom{{f(x)}}\right.$$f (x)$$\left.\vphantom{{f(x)}}\right\vert$$dx.

• $\mathbbm$L²(Ω) est complet pour tout Ω mesurable avec le norme
  | f|_{$\mathbbm$L²(Ω)} = $$\left(\vphantom{\int_{\Omega}\left\vert{f(x)}\right\vert^{2}dx}\right.$$$$\int_{{\Omega}}^{}$$$$\left\vert\vphantom{{f(x)}}\right.$$f (x)$$\left.\vphantom{{f(x)}}\right\vert^{{2}}_{}$$dx$$\left.\vphantom{\int_{\Omega}\left\vert{f(x)}\right\vert^{2}dx}\right)^{{\frac{1}{2}}}_{}$$.

• $\mathbbm$L^p(Ω), p≥1 est complet pour tout Ω mesurable avec le norme
  | f|_{$\mathbbm$L^p(Ω)} = $$\left(\vphantom{\int_{\Omega}\left\vert{f(x)}\right\vert^{p}dx}\right.$$$$\int_{{\Omega}}^{}$$$$\left\vert\vphantom{{f(x)}}\right.$$f (x)$$\left.\vphantom{{f(x)}}\right\vert^{{p}}_{}$$dx$$\left.\vphantom{\int_{\Omega}\left\vert{f(x)}\right\vert^{p}dx}\right)^{{\frac{1}{p}}}_{}$$.

• C¹([O, 1]) est complet pour sa norme usuelle
  | f|_C¹ = $$\sup_{{[0,1]}}^{}$$$$\left\vert\vphantom{{f(x)}}\right.$$f (x)$$\left.\vphantom{{f(x)}}\right\vert$$ + $$\sup_{{[0,1]}}^{}$$$$\left\vert\vphantom{{f^{\prime}(x)}}\right.$$f^′(x)$$\left.\vphantom{{f^{\prime}(x)}}\right\vert$$.
  Cela se généralise pour l'ensemble des fonctions de classe C¹ définies sur un compact de $\mathbbm$Rⁿ.

Quelques exemples d'espaces qui ne sont pas des espaces de Banach

• C¹([O, 1]) n'est pas complet pour la norme
  | f|_∞ = $$\sup_{{[0,1]}}^{}$$$$\left\vert\vphantom{{f(x)}}\right.$$f (x)$$\left.\vphantom{{f(x)}}\right\vert$$.

• C^$\mathbbm$R n'est même pas normable.
• C¹(]O, 1[) n'est même pas normable.