Sous-sections
Les espaces de Hilbert sont très importants car ils sont à la base des
théorèmes d'existence pour les problèmes issues de la Mécanique,
notamment en ce qui concerne les formulations variationnelles (ou
principe des puissances virtuelles) qui entrent dans le cadre de la
théorie de Lax-Milgram.
Définition 14.2.1
Soit H un espace vectoriel. Un produit scalaire sur H est une
forme bilinéaire définie positive symétrique a(u, v) de H×H à
valeur dans
 R. Une telle forme bilinéaire induit une norme
R. Une telle forme bilinéaire induit une norme
|
u|
a =
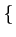 a
a(
u,
u)
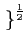
.
Définition 14.2.2
Soit H un espace vectoriel muni d'un produit scalaire, on dit que
H est un espace de Hilbert s'il est complet pour la norme associée
au produit scalaire.
Ainsi, un espace de Hilbert est un cas particulier d'espace de Banach.
-
 L2(Ω) est un Hilbert pour tout Ω
mesurable avec le produit scalaire :
L2(Ω) est un Hilbert pour tout Ω
mesurable avec le produit scalaire :
-
H1(Ω) est un Hilbert pour tout Ω
mesurable avec le produit scalaire :
(
f,
g)
 H1
H1 =
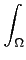 f
f (
x)
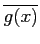 dx
dx +
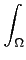
∇
f (
x).
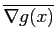 dx
dx
Théorème 14.2.3
Représentation de Riesz - Soit L une forme linéaire continue
définie sur un Hilbert H. Il existe un unique f∈H tel que
(f, v)H = L(v)∀v∈H.
Théorème 14.2.4
Soit H un espace de Hilbert séparable, alors il existe une suite
en∈H telle que
-
| en|H = 1
-
(en, em)H = δn, m
- l'espace vectoriel engendré par les en est dense dans H :
∀
u∈
H u =
 anen
anen
an = (u, en)H
et
choi
2008-12-22