Sous-sections
Déterminant de n vecteurs de
 Rn
Rn
Le théorème suivant est également une définition :
Théorème 3.5.1
Soit
E =  Rn, et soit
(
Rn, et soit
(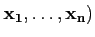 une
base de E. Il existe une unique n-forme alternée définie sur
En appelée déterminant telle que
une
base de E. Il existe une unique n-forme alternée définie sur
En appelée déterminant telle que
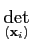
(
En désigne le produit d'espace
E×E×...×E
(n fois). Le déterminant étant alterné par définition, le
déterminant de n vecteurs de E change de signe si on permute deux
vecteurs :
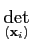
(

Par conséquent, le déterminant
de n vecteurs est nul si deux vecteurs sont égaux :
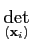
(
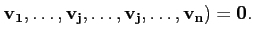
Plus généralement, si une famille de n vecteurs est lié,
c'est-à-dire que au moins un des vecteurs est une combinaison linéaire
des autres, par linéarité le déterminant est nécessairement nul.
Réciproquement, si une famille est libre, son déterminant est une
combinaison linéaire non nulle du déterminant de la base. On énonce
ainsi un critère pour déterminer si une famille de n vecteur de E
est une base de ou non :
Théorème 3.5.2
Une famille
(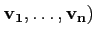 de n vecteurs de
E =
de n vecteurs de
E =  Rn , est une base de E si et seulement si
Rn , est une base de E si et seulement si
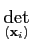
(
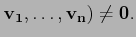
Dans toute la suite, on définira toujours le déterminant rapporté à la
base canonique de E plutôt qu'une base quelconque. Ainsi le
déterminant ne sera désigné que par le symbole det.
Soit A une matrice n×n, elle est donc constitué de n
colonnes de matrices n×1, chacune d'elles représentant un
vecteurs de
 Rn (ou n'importe quel espace vectoriel de
dimension n). Ainsi on peut définir le déterminant d'une matrice par
l'intermédiaire de ses vecteurs colonnes :
Rn (ou n'importe quel espace vectoriel de
dimension n). Ainsi on peut définir le déterminant d'une matrice par
l'intermédiaire de ses vecteurs colonnes :
Définition 3.5.3
Le déterminant d'une matrice carré est défini par le déterminant de
ses vecteurs colonnes.
Proposition 3.5.4
Soit I la matrice identité n×n, par définition det I = 1.
Proposition 3.5.5
Soit A une matrice carré n×n,
det A = det At
Proposition 3.5.6
Soient A et B deux matrices n×n. Bien que A et B ne
permutent pas en général, on a
det(AB) = det(BA) = det A det B.
Cette dernière propriété permet de définir d'un opérateur linéaire :
Soit f un opérateur linéaire sur E et soit A une représentation
matricielle de f dans une base
( et B la
représentation matricielle de f dans une autre base
(
et B la
représentation matricielle de f dans une autre base
( .
Par conséquent il existe une matrice de passage P de la base
(
.
Par conséquent il existe une matrice de passage P de la base
( vers la base
(
vers la base
( . Si bien que
. Si bien que
det A = det(P-1BP) = det(PP-1B) = det B.
Autrement dit, si on définit le déterminant d'un opérateur linéaire
par le déterminant de sa représentation matricielle dans une base, ce
déterminant est indépendant du choix de la base.
Définition 3.5.7
Soit f un opérateur linéaire sur E et soit A une représentation
matricielle de f dans une base
(
det f = det A.
Théorème 3.5.8
Un opérateur linéaire est bijectif ou inversible si et seulement si
son déterminant est non nul.
Soit A une matrice carré n×n dont les coefficients sont
aij. On définit des sous-matrices extraites de A utiles pour le
calcul d'un déterminant :
Définition 3.5.9
On appelle mineur de aij dans A, le déterminant de la sous
matrice extraite de A ôtée de la i-ème ligne et la j-ème
colonne. On le note
Δij.
Définition 3.5.10
On note ComA, la matrice dont les composantes notées Aij sont
les cofacteurs de A :
Aij = (- 1)i+jΔij.
On dit que ComA est la matrice des cofacteurs de
A.
Théorème 3.5.11
Soit A une matrice carré n×n dont les coefficients sont
aij et soient Aij ses cofacteurs.
On a alors le développement du déterminant suivant la i-ème ligne :
det
A =
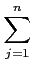 aijAij
aijAij,
det
A =
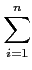 aijAij
aijAij.
Une conséquence immédiate est le calcul très simple du déterminant
d'une matrice triangulaire supérieure (resp. inférieure), i.e.
une matrice dont les coefficients au dessous (resp. au dessus) de la
diagonale sont tous nuls :
Proposition 3.5.12
Soit A une matrice carré triangulaire, son déterminant est le
produit de ses coefficients diagonaux.
Proposition 3.5.13
Soit A une matrice 2×2 de coefficients
aαβ,
det
A =
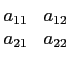

=
a11a22 -
a12a21.
Preuve : On vérifie aisément que la forme linéaire ainsi
définie est alternée et satisfait à det I = 1 où I désigne la
matrice identité. Par définition, c'est le déterminant.
Ainsi pour calculer le déterminant d'une matrice 3×3 on peut
développer suivant la 3-ème colonne (par exemple) :
On termine par une formule donnant l'inverse d'une matrice :
Théorème 3.5.14
Soit A une matrice carré n×n inversible, alors si A-1
désigne son inverse on a
A-1 =
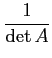
Com
At.
choi
2008-12-22
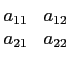
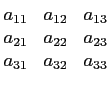
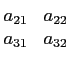
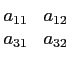
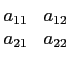
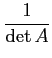 Com At.
Com At.