Sous-sections
Spectre d'un opérateur linéaire
L'ensemble des valeurs réelles λ pour lesquels l'application
[A - λI] est une bijection, est appelé ensemble
résolvant. Le complémentaire sur
 R de l'ensemble résolvant
est le spectre de A.
R de l'ensemble résolvant
est le spectre de A.
Remarque 3.6.2
Il est clair que l'ensemble des valeurs propres est contenu dans le
spectre. Cette inclusion est une égalité dans le cas où A opère sur
un espace de dimension finie, mais est stricte dans le cas général :
Pensez à l'opérateur shift dans l'espace vectoriel des suites
numériques de carré sommable : 0 est dans le spectre mais n'est pas
une valeur propre !
Définition 3.6.3
Soit A un opérateur linéaire sur
 Rn, le le déterminant
Rn, le le déterminant
PA(X) = det(A-XIn),
c'est un polynôme de degré n. On l'appelle polynôme
caractéristique de A.
Le polynôme caractéristique est utile dans la détermination des
valeurs propres d'un opérateur linéaire :
Proposition 3.6.4
Les racines du polynôme caractéristique d'un opérateur linéaire A
sont les valeurs propres de A.
Remarquons que les valeurs propres étant des racines d'un polynôme, il
est tout à fait possible qu'elles n'existent pas toutes dans
 R (c'est-à-dire que certaines sont complexes).
R (c'est-à-dire que certaines sont complexes).
Définition 3.6.5
On dit qu'un opérateur linéaire sur
 Rn est diagonalisable
si il existe une base de vecteurs propres. Dans une telle base la
représentation matricielle de A est une matrice diagonale composée
des valeurs propres de A.
Rn est diagonalisable
si il existe une base de vecteurs propres. Dans une telle base la
représentation matricielle de A est une matrice diagonale composée
des valeurs propres de A.
Proposition 3.6.6
Soit A un opérateur linéaire sur
 Rn, et soient
Rn, et soient
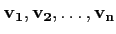 , une base de vecteurs
propres associées aux valeurs propres
λi. Soit D la
matrice, diagonale, dont tous les coefficients sur la diagonale est
constitués des valeurs propres
λ1, λ2,..., λn et dont tous les autres
coefficients sont nuls. Alors D est la représentation matricielle de
A dans la base de vecteurs propres associée.
, une base de vecteurs
propres associées aux valeurs propres
λi. Soit D la
matrice, diagonale, dont tous les coefficients sur la diagonale est
constitués des valeurs propres
λ1, λ2,..., λn et dont tous les autres
coefficients sont nuls. Alors D est la représentation matricielle de
A dans la base de vecteurs propres associée.
D =

Si de plus P est la matrice de passage d'une base
 vers la base de vecteurs
propres
vers la base de vecteurs
propres
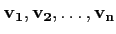 , alors la
représentation matricielle M de A dans la base
, alors la
représentation matricielle M de A dans la base
 est donné par :
est donné par :
M = PDP-1.
En général, un opérateur linéaire (resp. une matrice carrée) n'est pas
diagonalisable, il suffit de penser aux cas de valeurs propres
complexes. Il est cependant possible d'isoler quelques cas où il est
possible de diagonaliser :
Proposition 3.6.7
Soit A un opérateur linéaire sur E un espace vectoriel réel de
dimension n. Si les valeurs propres sont toutes distinctes et
réelles, alors A est diagonalisable.
Naturellement la proposition précédente n'est pas du tout une
condition nécessaire, est une application peut posséder des valeur
propres multiples et être diagonalisable : pensez à l'opérateur
identité.
Terminons par deux résultats très importants :
Théorème 3.6.8
Il est toujours possible de trigonaliser un opérateur
linéaire dans
 C (resp. une matrice carrée).
C (resp. une matrice carrée).
Il s'en suit le théorème
Théorème 3.6.9
Cayley-Hamilton - Soit A un opérateur linéaire sur
 Rn
et PA son polynôme caractéristique, alors
PA(A) = 0.
Rn
et PA son polynôme caractéristique, alors
PA(A) = 0.
En fait, la réduction d'un endomorphisme (un opérateur linéaire),
s'applique également lorsqu'on a pas diagonalisation : c'est la
décomposition spectrale.
Théorème 3.6.10
Soit A un opérateur linéaire sur
 Rn. On suppose que le
polynôme minimal de A est scindé (pas de racines complexes). Alors
on peut décomposer A = D + N où D est diagonale et N est
nilpotente. De plus N et D commutent. Cette décomposition est
unique.
Rn. On suppose que le
polynôme minimal de A est scindé (pas de racines complexes). Alors
on peut décomposer A = D + N où D est diagonale et N est
nilpotente. De plus N et D commutent. Cette décomposition est
unique.
Cas des matrices symétriques définies positives
Le cas des matrices symétriques définies positives est très utile en mécanique, puisque la
plupart des objets rencontrés comme les formes d'énergie de déformation élastique (tenseur
des contraintes, des déformations) pourront être représentées (dans leur version discrétisée) par de telles matrices, voir la méthode des éléments-finis par exemple.
Commençons par un résultat fondamental concernant les matrices symétriques:
Théorème 3.6.11
Soit A un opérateur linéaire autoadjoint (i.e, symétrique) de
 Rn alors A est diagonalisable et de plus il existe une
base orthonormée de vecteurs propres.
Rn alors A est diagonalisable et de plus il existe une
base orthonormée de vecteurs propres.
Preuve.
Principe de la preuve : par récurrence.

Définition 3.6.12
Soit A un opérateur linéaire sur
 Rn.
Rn.
On dit que A est positive si
∀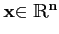 ,
A(
,
A(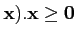 .
.
On dit que A est définie positive si il existe c > 0 telle que
∀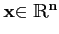 ,
A(
,
A(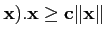 .
.
Ainsi, soit
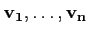 une base orthonormée de vecteurs propres associés aux valeurs propres λi d'une matrice symétrique A. Alors pour tout
une base orthonormée de vecteurs propres associés aux valeurs propres λi d'une matrice symétrique A. Alors pour tout
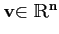 , il existe une décomposition unique
, il existe une décomposition unique
si bien que, si
λmin désigne la plus petite valeur propre,
(
A
Théorème 3.6.13
Soit A un opérateur linéaire sur
 Rn, A est définie
positive si et seulement si toutes ses valeurs propres sont
strictement positives.
Rn, A est définie
positive si et seulement si toutes ses valeurs propres sont
strictement positives.
choi
2008-12-22

![]()