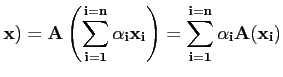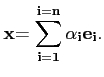Sous-sections
Preuve du théorème 1.2.4
Supposons que X soit de
dimension égale à n et soit
(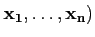 une
base de X. D'après la linéarité de A, l'image de A est engendré
par le système de n vecteurs
S = (A
une
base de X. D'après la linéarité de A, l'image de A est engendré
par le système de n vecteurs
S = (A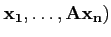 ,
on en déduit que S engendre X (autrement dit que A est
surjectif) si S est un système libre.
,
on en déduit que S engendre X (autrement dit que A est
surjectif) si S est un système libre.
Montrons que si A est injectif alors A est surjectif.
Si A est injectif, cela signifie que
A . Or si
. Or si
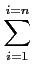 αi
αi
on a par linéarité de A
mais comme les
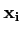 sont une famille libre, on obtient que les coefficients
αi sont nécessairement tous nuls. Autrement dit que le
système S est libre.
sont une famille libre, on obtient que les coefficients
αi sont nécessairement tous nuls. Autrement dit que le
système S est libre.
Réciproquement, montrons que si A est surjectif alors A est
injectif.
Si A est surjectif cela signifie que le système S est
libre. Alors si
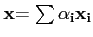 annule
l'opérateur A :
A
annule
l'opérateur A :
A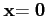 , alors par linéarité on a
, alors par linéarité on a
0 =
A(
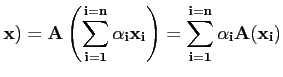
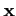 est nécessairement nul, ce qui prouve que A est injectif.
est nécessairement nul, ce qui prouve que A est injectif.
Preuve du théorème 1.2.8
- Soit
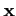 un vecteur tel
que
|
un vecteur tel
que
|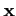 | = 1.
| = 1. 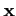 se décompose dans la base
canonique sous la forme
se décompose dans la base
canonique sous la forme
Puisque
|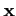 | =
| = 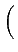
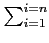 αi2
αi2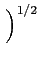 = 1. On
a alors nécessairement
= 1. On
a alors nécessairement
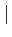 αi
αi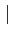 ≤1, d'où
≤1, d'où
|
A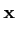
| = |
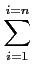 αiA
αiA(
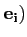
|≤
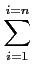
 αi
αi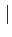
|
A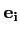
|≤
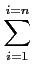
|
A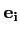
|≤
n < + ∞
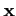 ,
,
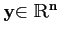 ,
| A
,
| A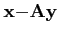 |≤| A||
|≤| A||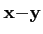 |, on en déduit
l'uniforme continuité.
|, on en déduit
l'uniforme continuité.
- De la linéarité de A, nous obtenons facilement
|(
A+
B)
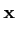
|≤|
A(
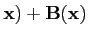
|≤|
A(
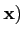
| + |
B(
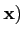
|≤(|
A| + (|
B|)|
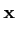
|
- Enfin, on a
|(
BA)
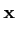
|≤|
B(
A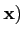
|≤|
B||
A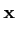
|≤|
B||
A||
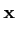
|
Preuve de la proposition 1.3.4
Soit
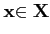 , de coordonnées
αi dans la base
(
, de coordonnées
αi dans la base
(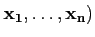 , d'après l'inégalité de Schwarz on a
, d'après l'inégalité de Schwarz on a
|
A(
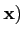
|
2 =
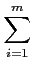
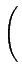
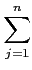 aijαj
aijαj
≤
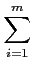
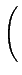
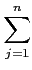 aij2
aij2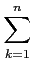 αk2
αk2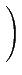
≤
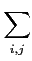 aij2
aij2|
x|
2.
choi
2008-12-22
![]() . Or si
. Or si
![]() annule
l'opérateur A :
A
annule
l'opérateur A :
A![]() , alors par linéarité on a
, alors par linéarité on a