Sous-sections
Fonction différentiable - Application dérivée
De façon classique on la définition pour une fonction d'une variable
réelle à valeur dans
 R:
R:
On dit que f est dérivable en x0 s'il existe un réel
f′(x0) défini par
f′(
x0) =
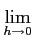
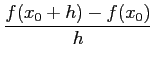
.
Cependant, comme pour la continuité, on va adopter une autre
présentation de la définition afin de la généraliser
Définition 4.3.1
On dit que f est dérivable en x0 s'il
existe un réel
f′(x0) tel que
f (x0 + h) - f (x0) = f′(x0)h + o(h)
le ``reste'' o(h) étant négligeable dans le sens que
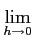
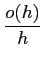
= 0.
On remarque que la quantité
f (x0 + h) - f (x0) s'exprime comme la
somme d'une application linéaire qui à h associe
f′(x0)h et d'un reste négligeable.
On peut donc considérer la dérivée de  au point x0 non seulement comme un réel mais également comme un opérateur linéaire
sur
au point x0 non seulement comme un réel mais également comme un opérateur linéaire
sur
 R qui à h associe
f′(x0)h (en fait cette
considération a été établi à partir de la bijection naturelle entre
R qui à h associe
f′(x0)h (en fait cette
considération a été établi à partir de la bijection naturelle entre
 R et
R et
 (
( R)).
R)).
C'est cette définition qu'il faudra retenir. En général, les étudiants
ont beaucoup de mal à oublier la définition qu'ils ont apprise dans le
Secondaire valable uniquement pour les fonctions réelles d'une
variable réelle, et ils l'utilisent sans scrupule même s'il n'a plus
de sens comme c'est le cas pour tout les autres cas de fonctions. Il
va sans dire que ce genre d'erreurs coûte quelques points aux
examens ;-)
Considérons maintenant une fonction  définie sur un intervalle
]a, b[ de
définie sur un intervalle
]a, b[ de
 R à valeurs dans
R à valeurs dans
 Rm. Rappelons que
cela signifie que
Rm. Rappelons que
cela signifie que
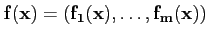 ou encore,
si on représente une base canonique de
ou encore,
si on représente une base canonique de
 Rm
par
{
Rm
par
{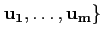 :
:
En un point
x0∈]a, b[, la dérivée de  en x0,
noté
en x0,
noté
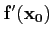 , est défini comme le vecteur de
, est défini comme le vecteur de
 Rm (si il existe) tel que
Rm (si il existe) tel que
Soulignons encore que l'égalité précédente est vectorielle :
et donc peut également s'écrire sous forme matricielle
dans la base canonique:
ou encore sous forme vectorielle :
Définition 4.3.2
 est dérivable en x0 si et seulement si il existe un
vecteur
est dérivable en x0 si et seulement si il existe un
vecteur
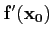 tel que :
tel que :
La dérivée de  en x0 apparaît non seulement comme un
vecteur de
en x0 apparaît non seulement comme un
vecteur de
 Rm mais également comme une application
linéaire de
Rm mais également comme une application
linéaire de
 R dans
R dans
 Rm qui associe à tout réel
h le vecteur
Rm qui associe à tout réel
h le vecteur
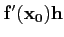 (il s'agit là de la
bijection naturelle entre
(il s'agit là de la
bijection naturelle entre
 Rm et
Rm et
 (
( Rm,
Rm, R)).
R)).
On va maintenant généraliser ces notions.
On dit alors que
 est la
différentielle (on ne dit plus dérivée?) de
est la
différentielle (on ne dit plus dérivée?) de  en
en  et on également parfois
et on également parfois
Ainsi, si  est différentiable sur un ouvert Ω, alors
pour tout
est différentiable sur un ouvert Ω, alors
pour tout
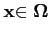 ,
,
i.e. la différentielle de  en
en  est une application
linéaire de
est une application
linéaire de
 Rn (tout entier) dans
Rn (tout entier) dans
 Rm mais on
peut remarquer que
Rm mais on
peut remarquer que
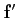 est une application de Ω
vers
est une application de Ω
vers
 (
( Rn,
Rn, Rm).
Rm).
Remarque 4.3.4
Pour des raisons, disons pédagogiques, nous nous sommes limités dans
le cadre de ces rappels aux fonctions définies sur des parties de
 Rn à valeurs dans
Rn à valeurs dans
 Rm. Mais, tout ce qui suit
est également valable si on remplace les
Rm. Mais, tout ce qui suit
est également valable si on remplace les
 Rn et
Rn et
 Rm par des objets ``plus abstraits'' que sont les
espaces de Banach (i.e. des espaces normés complets)
qu'on pourrait noter également E et F. Les énoncés et les
démonstrations demeurant strictement identiques.
Rm par des objets ``plus abstraits'' que sont les
espaces de Banach (i.e. des espaces normés complets)
qu'on pourrait noter également E et F. Les énoncés et les
démonstrations demeurant strictement identiques.
Remarque 4.3.5
On parle également d'application tangente pour désigner la
différentielle en un point.
Théorème 4.3.6
Soit  une application d'un ouvert Ω de
une application d'un ouvert Ω de
 Rn
dans
Rn
dans
 Rm. Si
Rm. Si  est différentiable en
est différentiable en
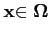 , alors sa différentielle est unique.
, alors sa différentielle est unique.
Preuve.
Supposons qu'on ait, avec
t∈ R
R,
f (x + th) = f (x) + df1th + o(th) et f (x + th) = f (x) + df2th + o(th)
Alors on obtient en effectuant la différence:
(df1 - df2)th = o(th) = t2o(h)
d'où pour tout
t
(df1 - df2)h = to(h)
c'est à dire
(df1 - df2)h = 0

Quelques remarques
- Si
 est différentiable en
est différentiable en  alors
alors  est
nécessairement continue en
est
nécessairement continue en  (exercice).
(exercice).
- La différentielle notée
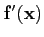 ou
d
ou
d
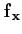 est appelée parfois dérivée totale de
est appelée parfois dérivée totale de  en
en  , afin de la distinguer des dérivées partielles.
, afin de la distinguer des dérivées partielles.
- Si
A∈
 (
( Rn,
Rn, Rm) et si
x∈
Rm) et si
x∈ Rn alors
Rn alors
A′(
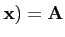
Autrement dit, une application linéaire est sa propre différentielle.
Remarquez que  apparaît explicitement dans le premier membre
mais pas dans le second : c'est parce que la fonction dérivée d'une
application linéaire est constante (indépendance par rapport au
``point'' où on dérive.
apparaît explicitement dans le premier membre
mais pas dans le second : c'est parce que la fonction dérivée d'une
application linéaire est constante (indépendance par rapport au
``point'' où on dérive.
Remarquer que le second membre est le produit de deux applications
linéaires :
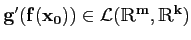 et
et
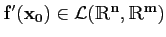 ;
on a bien que
;
on a bien que
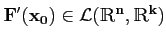 .
.
Preuve.

Puisque la différentielle de  en un point est une application
linéaire de
en un point est une application
linéaire de
 Rn vers
Rn vers
 Rm, on peut la
représenter sous forme matricielle. Plus précisément par une matrice
n×m.
Soient
(
Rm, on peut la
représenter sous forme matricielle. Plus précisément par une matrice
n×m.
Soient
(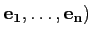 et
(
et
(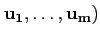 les bases canoniques des espaces
les bases canoniques des espaces
 Rn et
Rn et
 Rm respectivement:
Rm respectivement:
Définition 4.3.8
La représentation matricielle de la différentielle de  dans
ces bases canoniques est la matrice Jacobienne. Usuellement, elle est
notée
J(
dans
ces bases canoniques est la matrice Jacobienne. Usuellement, elle est
notée
J(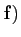 ou encore
J
ou encore
J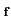 .
.
Définition 4.3.9
Soit xj la j-ème variable de
 Rn, la dérivée
partielle de
Rn, la dérivée
partielle de  par rapport à xj est la dérivée de
par rapport à xj est la dérivée de
 par rapport à xj, les autres variables étant
considérées fixes. On la note :
par rapport à xj, les autres variables étant
considérées fixes. On la note :
On peut remarquer qu'on a encore
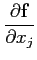
(
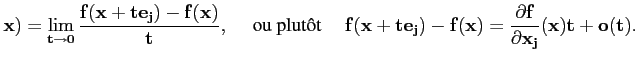
Proposition 4.3.10
Si  est différentiable en
est différentiable en  et si
et si
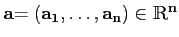 , alors toutes les
dérivées partielles existent et
, alors toutes les
dérivées partielles existent et
Attention: la réciproque n'est pas vrai : On peut construire une
fonction dont les dérivées partielles existent et sont continues mais
qui n'est pas elle même différentiable.
On note aussi parfois :
d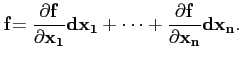
Théorème 4.3.11
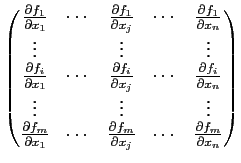
La composante de la i-ème ligne et de la j-ème colonne de la
matrice Jacobienne est la dérivée partielle de la i-ème composante
de  par rapport à la j-ème variable. On note :
par rapport à la j-ème variable. On note :
Jij =
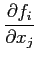
.
ou encore
(
J) =
.
 par rapport à la j-ème variable
xj.
par rapport à la j-ème variable
xj.
choi
2008-12-22
![]() R:
R:
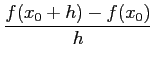 .
.
![]() définie sur un intervalle
]a, b[ de
définie sur un intervalle
]a, b[ de
![]() R à valeurs dans
R à valeurs dans
![]() Rm. Rappelons que
cela signifie que
Rm. Rappelons que
cela signifie que
![]() ou encore,
si on représente une base canonique de
ou encore,
si on représente une base canonique de
![]() Rm
par
{
Rm
par
{![]() :
:
![]() en x0,
noté
en x0,
noté
![]() , est défini comme le vecteur de
, est défini comme le vecteur de
![]() Rm (si il existe) tel que
Rm (si il existe) tel que
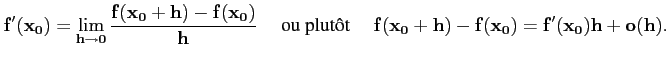
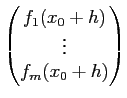 -
- 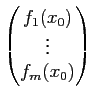 =
=  + o(h),
+ o(h),
 = 0.
= 0.
![]() est la
différentielle (on ne dit plus dérivée?) de
est la
différentielle (on ne dit plus dérivée?) de ![]() en
en ![]() et on également parfois
et on également parfois
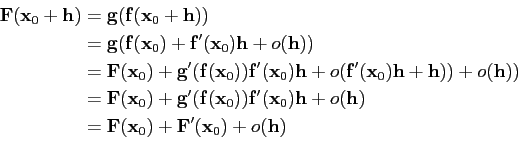
![]()

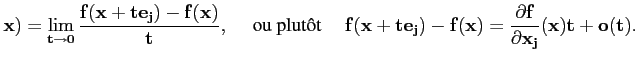
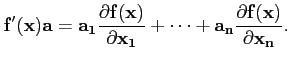
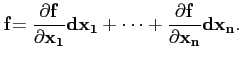
 .
.