Sous-sections
Gradient
La matrice Jacobienne étant relative aux bases canoniques, il est
important, afin de faire du calcul dans des bases autres que les
canoniques (telles que les coordonnées cylindriques...), de se rappeler
l'objet intrinsèque dont elle est le représentant. Il s'agit du
gradient de 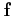 , qui n'est autre que l'application dérivée :
, qui n'est autre que l'application dérivée :
mais qui est aussi parfois défini par
d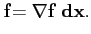
ou encore si les
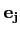 désignent une base fixe et si les
désignent une base fixe et si les
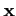 se décomposent dans cette base :
se décomposent dans cette base :
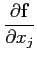
(
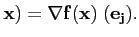
Ainsi la représentation
matricielle du gradient de 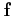 dans les bases canoniques est la
matrice Jacobienne.
dans les bases canoniques est la
matrice Jacobienne.
Divergence
Dans le cas particulier où n = m, la matrice Jacobienne est une
matrice carré. On peut alors définir de nouveaux opérateurs voir le paragraphe 4.4 sur la divergence dans le chapitre sur le théorème de Stokes :
Proposition 4.4.1
L'opérateur divergence est la trace du gradient :
div 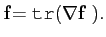
Toujours dans le cas où n = m,
Proposition 4.4.2
Le rotationnel de 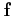 , noté
, noté
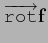 , est
le vecteur associé à la partie antisymétrique du gradient de
, est
le vecteur associé à la partie antisymétrique du gradient de
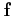 . Dans
. Dans
 R3, on a :
R3, on a :
[
Remarque 4.4.3
Dans la littérature mathématique, le gradient d'une fonction scalaire à plusieurs variables est souvent représentée par un vecteur, ainsi si
f (x) = f (x1,..., xn)∈ R, le gradient est défini par
R, le gradient est défini par
si bien qu'il est noté
∇
f (
x) =
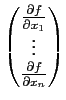
Remarque 4.4.4
L'opérateur divergence est parfois noté (sur wikipédia, dans de nombreux livres, surtout en physique) comme un produit scalaire par un pseudo vecteur ∇, mais c'est un abus d'écriture : cette notation n'est pas une définition et ne peut pas s'étendre à d'autres objets que des fonctions vectorielles, notamment la divergence d'un tenseur si importante en Mécanique.
Terminons ce paragraphe par quelques propriétés sur la divergence et le rotationnel :
Proposition 4.4.5
Pour tout champ de vecteur défini sur
Ω⊂ R3 à valeur dans
R3 à valeur dans
 R3 :
R3 :
|
= 0 |
(4.1) |
| ( |
= |
(4.2) |
|
= ∇div |
(4.3) |
Théorème 4.4.6
Si un champ de vecteur  , défini de
Ω⊂
, défini de
Ω⊂ Rn à valeur dans
Rn à valeur dans
 Rn, est tel que
alors il existe une fonction scalaire f définie sur Ω telle que
Rn, est tel que
alors il existe une fonction scalaire f définie sur Ω telle que
On dit que  dérive d'un potentiel.
dérive d'un potentiel.
De façon analogue, on a
Théorème 4.4.7
Si un champ de vecteur  , défini de
Ω⊂
, défini de
Ω⊂ Rn à valeur dans
Rn à valeur dans
 Rn, est tel que
div alors il existe un champs
Rn, est tel que
div alors il existe un champs 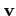 tel que
tel que
choi
2008-12-22