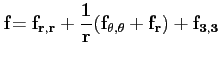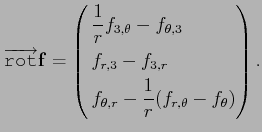Sous-sections
Nous terminons ce chapitre sur le calcul différentiel par des
expressions particulièrement utiles en Mathématiques appliquées, les
expressions des différents opérateurs différentiels en coordonnées
cylindriques et en coordonnées sphériques.
Plaçons dans
E =  R3 et désignons par
(
R3 et désignons par
( vecteur de la base canonique
de
vecteur de la base canonique
de
 R3 et désignons par O le point (0,0,0). Tout point
M de E peut être défini par son vecteur position
R3 et désignons par O le point (0,0,0). Tout point
M de E peut être défini par son vecteur position 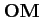 , dont
on donne les coordonnées dans la base canonique :
, dont
on donne les coordonnées dans la base canonique :
notation que l'on préfère à :
On définit les coordonnées cylindriques par
r =
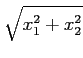
,
θ = arctan

,
x3 =
x3.
Alors le vecteur position se ré écrit :
où
En associant de plus le vecteur
on aura défini une base
( orthonormée de E, appelé base base cylindrique. Les coordonnées
(r, θ, x3) sont les coordonnées cylindriques de M.
orthonormée de E, appelé base base cylindrique. Les coordonnées
(r, θ, x3) sont les coordonnées cylindriques de M.
Considérons maintenant une fonction f définie sur une partie de
 R3, adoptons la notation abusive :
R3, adoptons la notation abusive :
f (x1, x2, x3) = f (r, θ, x3).
Nous notons également le produit scalaire de deux vecteurs (colonnes) indifféremment des trois manières suivantes :
Rappelons nous que nous avions identifié
puisque la variation de
(x1 + h, x2, x3) à
(x1 + h, x2, x3) est
h .
.
Le problème avec les coordonnées cylindriques est que si la variation
de
(r + δr, θ, x3) à
(r, θ, x3) est bien de
δr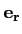 , ce qui entraîne
, ce qui entraîne
en revanche la variation de
(r, θ + δθ, x3) à
(r, θ, x3) n'est malheureusement pas
δθ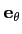 , ce qui signifie que
, ce qui signifie que
Plus précisément, si M est un point de coordonnées cylindrique
(r, θ, x3), et
M′ un point de coordonnées
(r, θ + δθ, x3) alors la variation
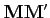 est en fait:
est en fait:
D'où nous avons :
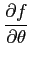
(
r,
θ,
x3) = ∇
f ⋅
r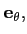
autrement dit les composantes cylindriques de
∇f sont :
∇
f =
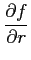
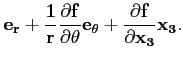
Considérons maintenant une fonction  définie sur une partie
de
définie sur une partie
de
 R3, et à valeur dans
R3, et à valeur dans
 R3 adoptons
également la notation abusive :
R3 adoptons
également la notation abusive :
On décomposera  dans les coordonnées cylindriques par
dans les coordonnées cylindriques par
D'après leur définition, il est facile de voir que
Ainsi,
On en déduit alors l'expression du gradient d'une fonction vectorielle
en composantes cylindriques :
∇
=
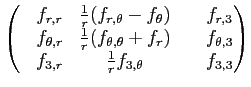
.
div 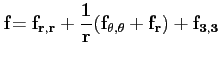
D'où le Laplacien d'une fonction scalaire en coordonnées cylindriques
Δf =
f, rr +
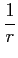
(
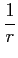 f, θθ
f, θθ +
f, r) +
f, 33.
Le rotationnel étant le vecteur associé à la partie
antisymétrique du gradient, on a
C'est la même chose qu'en cylindrique, sauf qu'il y a encore plus de
calcul à faire :-((
Si f est une fonction scalaire :
∇
f = (
fr,
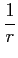 fθ
fθ,
fφ)
∇
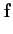
= .
choi
2008-12-22
![]() R3 et désignons par
(
R3 et désignons par
(![]() vecteur de la base canonique
de
vecteur de la base canonique
de
![]() R3 et désignons par O le point (0,0,0). Tout point
M de E peut être défini par son vecteur position
R3 et désignons par O le point (0,0,0). Tout point
M de E peut être défini par son vecteur position ![]() , dont
on donne les coordonnées dans la base canonique :
, dont
on donne les coordonnées dans la base canonique :
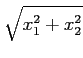 , θ = arctan
, θ = arctan![\begin{equation*}\begin{aligned}
&\vec{u} \cdot \vec{v}\\
&[\vec{u}]^\bot [\vec{v}] \\
&(\vec{u},\vec{v})
\end{aligned}\end{equation*}](img324.png)
 = ∇f ⋅
= ∇f ⋅![]() , ce qui entraîne
, ce qui entraîne
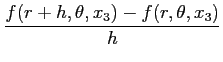 = ∇f ⋅
= ∇f ⋅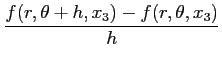 ≠∇f ⋅
≠∇f ⋅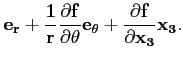
![$\displaystyle \begin{array}[c]{c}
f_{,r} \frac{1}{r} f_{,\theta} f_{,3}
\end{array}$](img347.png)
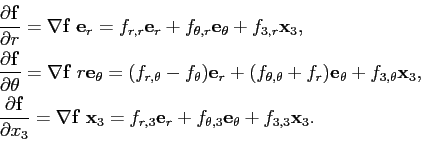
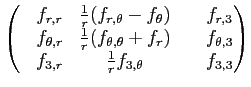 .
.