suivant: Théorème de Stokes et monter: Intégrale de Riemann précédent: Intégrale sur un pavé Table des matières Index
On généralise naturellement la définition de l'intégrale sur un pavé à
tout domaine se décomposant en une réunion finies et disjointe de
pavés. Plus généralement pour domaine
ω⊂![]() Rn on
peut trouver une suite de domaine
ωn qui sont chacun des
décompositions finies de pavés disjoints de
Rn on
peut trouver une suite de domaine
ωn qui sont chacun des
décompositions finies de pavés disjoints de
![]() Rn. Alors,
Rn. Alors,
Par ailleurs si un domaine Ω est l'image d'un pavé D par une application T :
où
Exemples :
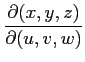 =
= 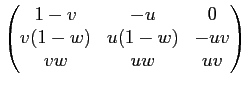
choi 2008-12-22