Sous-sections
Définition 10.3.1
Soit f une fonction à valeur réelle définie sur
E⊂ Rn. On dit que f est mesurable si pour tout
a∈
Rn. On dit que f est mesurable si pour tout
a∈ R,
R,
{x∈E / f (x) > a}
est un ensemble mesurable.
Proposition 10.3.2
Toute fonction continue sur E est mesurable dans E.
Théorème 10.3.3
Une f est mesurable si et seulement si pour tout
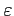 > 0 il existe une fonction continue
> 0 il existe une fonction continue 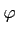 telle que
telle que
Autrement dit, les fonctions mesurables sont toutes les limites
simples de fonctions continues. Cela entraîne immédiatement le
résultat corollaire :
Corollaire 10.3.4
Toute limite simple de fonction mesurable est mesurable.
Théorème 10.3.5
Si f est une fonction mesurable sur E, et si fn
désigne une suite de fonctions mesurables sur E, alors les fonctions
-
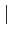 f
f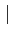
-
g(x) =
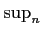 fn(x)
fn(x)
-
h(x) =
 supfn(x)
supfn(x)
le sont également.
Définition 10.3.6
On dit qu'une fonction mesurable f est nulle presque partout sur E
si il existe un ensemble de mesure nulle A tel que
f (
x) = 0 ∀
x∈
E 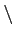 A
A.
On note f = 0 p.p. sur E.
Comme l'union finie d'ensembles de mesure nulle est également de
mesure nulle, on peut définir la relation d'équivalence
f∼
g sur
E  f
f -
g = 0 p.p. sur
E
choi
2008-12-22