Ensemble mesurable

Mesure extérieure

Définition 10.2.1   Soit A une partie de E⊂$\mathbbm$Rⁿ, on définit sa mesure extérieure par

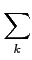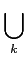μ^*(A) = inf{$$\sum_{{k}}^{}$$m(P_k);    A⊂$$\bigcup_{{k}}^{}$$P_k.}

où A⊂∪_kP_k désigne un recouvrement de A par des pavés de E.

Ensemble mesurable

Définition 10.2.2   Une partie A de E est dit mesurable si pour tout 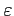$\varepsilon$ > 0, il existe un ensemble élémentaire B de E tel que

μ^*(AΔB)≤$$\varepsilon$$

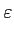
où AΔB désigne la différence symétrique ^10.1.

Autrement dit, les ensembles mesurables sont les ensembles limites d'ensembles élémentaires. Ce qui signifie que pour trouver un ensemble non-mesurable, il faut se lever de bonne heure !

Malgré tout nous pouvons préciser un peu la définition d'ensemble mesurable. De façon triviale nous avons

Proposition 10.2.3   Tout ensemble élémentaire est mesurable.

Théorème 10.2.4   Tout ensemble ouvert de ⊂$\mathbbm$Rⁿ est mesurable

Preuve du théorème 8.2.4 : Soit A un ouvert de E. Par définition, pour chaque point de A, il existe une boule (et donc un pavé) de mesure non-nulle, centré en ce point et contenu dans A.

Il suffit alors de considérer tous les points de A à composantes rationnelles et les pavés de cotés rationnels. Il est clair que tous les points de A sont contenus dans un de ces pavés ``rationnels''. Ce qui signifie que A peut être approchée par des ensembles élémentaires aussi près que l'on veut. $\Box$

Théorème 10.2.5   La réunion dénombrable d'ensembles mesurables est mesurable. L'intersection finie d'ensembles mesurables est mesurable.

Mesure d'un ensemble mesurable

Définition 10.2.6   Soit A un ensemble mesurable dans E. Alors la mesure de A est sa mesure extérieure.

m(A) = μ^*(A).

Proposition 10.2.7   Soit A_n des ensembles mesurables et soit A = ∪_nA_n. Alors

m(A)≤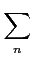$$\sum_{{n}}^{}$$m(A_n).

Si de plus les A_n sont deux à deux disjoints, alors

m(A) = 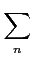$$\sum_{{n}}^{}$$m(A_n).

Ensemble de mesure nulle

Nous terminons cette section par des exemples d'ensemble de mesure nulle. A compléter..