Fonctions étagées

Fonctions élémentaires

Définition 11.1.1 Une fonction élémentaire de E est une fonction valant 1 sur une partie mesurable de E et 0 partout ailleurs. On parle aussi de fonctions indicatrices^11.1. Par exemple

$\displaystyle \mathbbm$ 1_A(x) = $\displaystyle \left\{\vphantom{ \begin{array}[c]{ll} 1 & \mbox{ si } x\in A \\ 0 & \mbox{ si } x\notin A. \end{array}}\right.$ $\displaystyle \begin{array}[c]{ll} 1 & \mbox{ si } x\in A \\ 0 & \mbox{ si } x\notin A. \end{array}$

En général, de telles fonctions peuvent également être définies sur des ensembles non-mesurables. Nous choisissons une telle restriction car les ensembles non mesurables ne nous intéressent pas. Pour ne pas être gênés, nous les excluons tout simplement de notre étude. Cela est légitime car ces ensembles ne jouent aucun rôle dans la théorie de Lebesgue.

Fonctions étagées

Définition 11.1.2 On appelle fonction étagée toute fonction définie par une combinaison linéaire de fonctions élémentaires ou indicatrices.

Ainsi, f est étagée si il existe des ensembles mesurables A_i et des scalaires α_i tel que

f (x) = 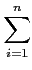$\displaystyle \sum_{{i=1}}^{{n}}$ α_i $\displaystyle \mathbbm$ 1_{A_i}.

Théorème 11.1.3 Les fonctions étagées sont denses dans l'ensemble des fonctions mesurables.

Autrement dit, les fonctions mesurables peuvent être considérées comme des limites simples de fonctions étagées.

Preuve du théorème 9.1.3 - Soit f une fonction mesurable sur E, sans perte de généralités, on suppose que f≥ 0.

On définit alors les ensembles mesurables, pour n∈ $\mathbbm$ N^* et i = 1, 2, 3,..., n2ⁿ:

E_ni	= {x∈E / (i - 1)2^-n≥f (x)≥i2^-n}
F_n	= {x∈E / f (x)≥n}.

Nous construisons alors la suite de fonctions de fonctions étagées

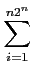
f_n = $\displaystyle \sum_{{i=1}}^{{n2^{n}}}$ (i - 1)2^-n $\displaystyle \mathbbm$ 1_{E_ni} + n $\displaystyle \mathbbm$ 1_{F_n}.

Il est facile de voir que pour tout n

f_n≥f_n+1≥...≥f

et que par construction, pour tout x∈E

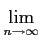$\displaystyle \lim_{{n\rightarrow \infty}}^{}$ f_n(x) = f (x) $\displaystyle \Box$

Remarquons que dans la démonstration, la convergence est uniforme si f est bornée.

Intégrale d'une fonction étagée

Définition 11.1.4 Soit 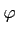$\varphi$ une fonction étagée :

$\displaystyle \varphi$ (x) = $\displaystyle \sum_{{i=1}}^{{n}}$ α_i $\displaystyle \mathbbm$ 1_{A_i}(x).

Si ω est un ensemble mesurable, alors

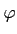
I_Ω( 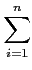$\displaystyle \varphi$ ) = $\displaystyle \sum_{{i=1}}^{{n}}$ α_im(A_i∩Ω)

est l'intégrale de 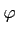$\varphi$ sur Ω.

Intégrale de Lebesgue d'une fonction mesurable

La définition 9.1.4 induit la définition de l'intégrale de Lebesgue

Définition 11.1.5 Soit f une fonction mesurable sur E positive et soit Ω une partie mesurable de E.

L'intégrale de Lebesgue de f sur Ω est la borne supérieure des intégrales sur Ω des 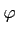$\varphi$ , fonctions étagées positives majorées par f:

$\displaystyle \int_{{\Omega}}^{}$ f = $\displaystyle \sup_{{\varphi}}^{}$ I_Ω( $\displaystyle \varphi$ )

Remarque 11.1.6 On note indifféremment :

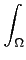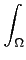$\displaystyle \int_{{\Omega}}^{}$ f = $\displaystyle \int_{{\Omega}}^{}$ f (x)dx

où x joue le rôle d'une variable muette.

Proposition 11.1.7 Soit f fonction mesurable sur E positive et soit Ω une partie mesurable de E. Si f_n désigne la suite de fonctions positives étagées introduite dans la démonstration du théorème 9.1.3, alors

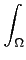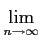$\displaystyle \int_{{\Omega}}^{}$ f = $\displaystyle \lim_{{n\rightarrow \infty}}^{}$ I_Ω(f_n).

Remarque 11.1.8 Ainsi définie, l'intégrale peut tout à fait prendre une valeur infinie.

Pour une fonction mesurable f désignons par f⁺ et f^- deux fonctions mesurables et positives qui sont respectivement ses parties positive et négatives:

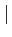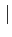f⁺(x)	= $\displaystyle \left\vert\vphantom{{f(x)}}\right.$ f (x) $\displaystyle \left.\vphantom{{f(x)}}\right\vert$ $\displaystyle \mathbbm$ 1_E⁺(x)
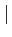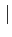f^-(x)	= $\displaystyle \left\vert\vphantom{{f(x)}}\right.$ f (x) $\displaystyle \left.\vphantom{{f(x)}}\right\vert$ $\displaystyle \mathbbm$ 1_E^-(x)

où

E⁺	= {x∈E / f (x)≥0}
E^-	= {x∈E / f (x)≤0}.

Si bien que pour tout x∈E

f (x) = f⁺(x) - f^-(x).

Cette décomposition permet de définir l'intégrale (de Lebesgue) pour toute fonction mesurable :

Définition 11.1.9 Soit f une fonction mesurable sur E, alors pour tout Ω⊂E mesurable, on définit

$\displaystyle \int_{{\Omega}}^{}$ f = $\displaystyle \int_{{\Omega}}^{}$ f⁺ - $\displaystyle \int_{{\Omega}}^{}$ f^-.

Définition 11.1.10 On dit qu'une fonction mesurable f est Lebesgue intégrable ou sommable sur E si

$\displaystyle \int_{{E}}^{}$ $\displaystyle \left\vert\vphantom{{f}}\right.$ f $\displaystyle \left.\vphantom{{f}}\right\vert$ < + ∞.

On note par $\mathscr$ L¹(E) l'ensemble des fonctions Lebesgue-intégrable sur E.

Le résultat suivant est fondamental :

Théorème 11.1.11 L'intégrale sur Ω d'une fonction positive f est nulle si et seulement si f est nulle presque partout sur Ω :

$\displaystyle \int_{{\Omega}}^{}$ $\displaystyle \left\vert\vphantom{{f}}\right.$ f $\displaystyle \left.\vphantom{{f}}\right\vert$ = 0 $\displaystyle \Longleftrightarrow$ f = 0 p.p. sur Ω.

choi 2008-12-22