... Choï1.1
choi@meca.unicaen.fr 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... abstraite3.1
Comme on pourra le remarquer, en Mathématique plus on est abstrait et plus on est précis ;-)... C'est comme ça! Et encore: ici, nous nous sommes restreint aux cas réel ou complexe... 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... savant3.2
la notion d'application linéaire peut être considérée comme le prolongement d'un homomorphisme de groupe à un espace vectoriel 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... suite3.3
c'est l'opérateur shift en anglais 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...M3.4
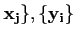On le note également d'autres façon telles que (A) ou encore M ou bien [A], pour être tout à fait rigoureux il faudrait indiquer Mat(A, {$ \bf{x}{_{j}\},\{\vec {y}_{i}\}$); c'est-à-dire indiquer la matrice de l'application linéaire A de la base de départ {$ \bf{x}{_{j}\}$ dans la base d'arrivée {$ \bf{y}{_{i}\}$. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
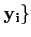... symétrique10.1
AΔB = [A 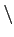$ \setminus$ (A∩B)]∪[B 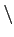$ \setminus$ (A∩B)] 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... indicatrices11.1
On parle également de fonctions caractéristiques mais nous ne recommandons pas cette appellation 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.