Sous-sections
Théorème de convergence monotone
Théorème 11.2.1
Soient
f1,..., fn,... des fonctions mesurables positives
sur E telles que
0≤f1≤...≤fn≤fn+1≤...
Posons
f (
x) =
 fn
fn(
x).
Alors
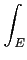 fn
fn→
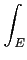 f
f.
Preuve du théorème 9.2.1 : Posons
αn =
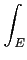 fn
fn.
Alors, puisque la suite fn est croissante, les
αn
convergent vers une limite
αn→α∈[0, + ∞].
Par définition f domine les fn, ainsi
α≤
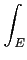 f
f.
Soit  une fonction étagée positive et dominée par f et soit
0 < a < 1. Si on pose
une fonction étagée positive et dominée par f et soit
0 < a < 1. Si on pose
En = {
x∈
E /
fn(
x)≥
a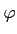
(
x)},
il est clair que
En⊂En+1 et
E = ∪nEn.
D'où pour tout n,
Autrement dit, pour tout  dominé par f et pour tout 0 < a < 1,
dominé par f et pour tout 0 < a < 1,
Si bien qu'on a montré que
α =
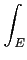 f
f.

Une conséquence du théorème de convergence monotone 9.2.1 est le
Lemme 11.2.2
Soient fn des fonctions mesurables sur E et positives. Si
f (
x) =
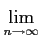
inf
fn(
x) =
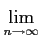
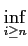
{
fi(
x)},
alors
Preuve du lemme de Fatou : Posons
gn(
x) =
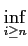
{
fi(
x)}.
Par définition,
0≤g1(x)≤g2(x)≤...≤gn(x).
Alors, d'après le théorème 9.2.1 de convergence monotone,
Théorème de convergence dominée
Théorème 11.2.3
Soient
fn∈ L1(E), une suite de fonctions sommable sur E telles que
L1(E), une suite de fonctions sommable sur E telles que
-
fn(x)→f (x) p.p. sur E
-
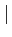 fn
fn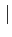 ≤g∈
≤g∈ L1(E)
L1(E)
Alors
f∈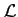 1(E) et
1(E) et
C'est le résultat central de la théorie de Lebesgue. Il en découle tous les
théorèmes de passage à la limite.
Son avantage par rapport à la
théorie classique de Riemann, c'est son énoncé valable pour tout
type de domaine E pourvu qu'il soit mesurable. Son application est
aisé puisqu'il ne demande qu'une domination.
De plus, c'est un résultat optimal
Preuve du théorème 9.2.3 de convergence dominée :
Puisque
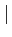 fn
fn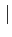 ≤g∈
≤g∈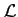 1(E) cela signifie
que f≤g et donc que
f∈
1(E) cela signifie
que f≤g et donc que
f∈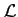 1(E).
1(E).
D'autre part, puisque
fn + g≥ 0, le lemme de fatou
9.2.2 indique
Ce qui implique, en retranchant g :
Mais on a également que
g - fn≥ 0 si bien que
qui entraîne, toujours en retranchant g :
D'où
En conclusion, on a montré que
Cela prouve que la limite existe et que cette limite vaut
Théorème 11.2.4
Soit f (x, y) une fonction mesurable et dérivable par rapport à y
pour presque tout x∈E, telle que cette dérivée partielle est
mesurable dans E. Si
alors
Théorème 11.2.5
Soit f une fonction mesurable dans le domaine
Ωx×Ωy. Si
0≥f < + ∞ , et si
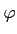
(
x) =
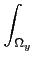 f
f (
x,
y)
dy ψ(
y) =
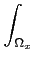 f
f (
x,
y)
dx
alors  et ψ sont mesurables et
et ψ sont mesurables et
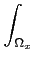
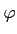
(
x)
dx =
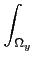 ψ
ψ(
y)
dy =
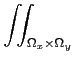 f
f (
x,
y)
dxdy
Théorème 11.2.6
Formule de Jacobi
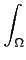 f
f (
x)
dx =
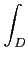 f
f (
T(
u))
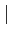 JT
JT(
u)
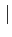 du
du
où
 JT(u)
JT(u)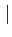 est la Jacobienne (déterminant du gradient ou
Jacobien) de l'application T(u) = x.
est la Jacobienne (déterminant du gradient ou
Jacobien) de l'application T(u) = x.
choi
2008-12-22
![]() fn
fn![]() ≤g∈
≤g∈![]() 1(E) cela signifie
que f≤g et donc que
f∈
1(E) cela signifie
que f≤g et donc que
f∈![]() 1(E).
1(E).

 dx.
dx.
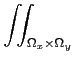 f (x, y)dxdy
f (x, y)dxdy