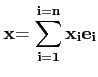Sous-sections
Espaces vectoriels
Un espace vectoriel est un ensemble d'éléments
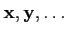 , appelés vecteurs, sur lequel sont
définis les opérations linéaires : une addition et une
multiplication par un scalaire (un nombre réel ou complexe),
avec les règles usuelles liées à la notion d'addition et de
multiplication :associativité, commutativité, élément neutre,
transitivité,...
, appelés vecteurs, sur lequel sont
définis les opérations linéaires : une addition et une
multiplication par un scalaire (un nombre réel ou complexe),
avec les règles usuelles liées à la notion d'addition et de
multiplication :associativité, commutativité, élément neutre,
transitivité,...
Dans le jargon mathématicien l'addition désigne une opération interne
entre deux vecteurs donnant un vecteur, tandis que la multiplication
est une opération externe entre un scalaire et un vecteur donnant
encore un vecteur.
On parle d'espace vectoriel réel si les scalaires sont les
nombres réels. De même, on parle d'espace vectoriel complexe si les
scalaires sont les nombres complexes. Dans toute la suite, sauf
mention contraire, les espaces vectoriels seront réels.
- Le premier exemple d'espace vectoriel réel est l'ensemble des
nombres réels
 R lui-même, avec évidemment les addition et
multiplication usuelles. Dans ce cas particulier, les nombres réels
sont à la fois considérés comme des scalaires et comme des
vecteurs en tant qu'éléments de l'espace vectoriel.
R lui-même, avec évidemment les addition et
multiplication usuelles. Dans ce cas particulier, les nombres réels
sont à la fois considérés comme des scalaires et comme des
vecteurs en tant qu'éléments de l'espace vectoriel.
Il en va de même pour l'ensemble des nombres complexes
 C.
Cependant, dans ce cas, on peut distinguer deux possibilités :
C.
Cependant, dans ce cas, on peut distinguer deux possibilités :
 C en tant qu'espace vectoriel complexe, ou bien
C en tant qu'espace vectoriel complexe, ou bien
 C en
tant qu'espace vectoriel réel (on parle de plan complexe pour cette
dernière).
C en
tant qu'espace vectoriel réel (on parle de plan complexe pour cette
dernière).
- Autre exemple, l'ensemble des fonctions définies sur un
intervalle de
I⊂
 R à valeur réelle: on définit
naturellement l'addition de deux fonctions f et g par :
R à valeur réelle: on définit
naturellement l'addition de deux fonctions f et g par :
h = f + g ⇔ h(x) = f (x) + g(x) ∀x∈I.
La multiplication d'une fonction f par un scalaire λ est définie par
h = λf ⇔ h(x) = λf (x) ∀x∈I.
En fait dans cet exemple, un point crucial est que l'addition est une
opération interne : autrement dit, l'addition de deux fonctions doit
encore être une fonction définie sur I à valeur réelle. Il en va de
même pour la multiplication. C'est ce qu'on appelle la
stabilité linéaire.
Une conséquence est qu'un espace vectoriel contient nécessairement un
élément neutre pour l'addition, à savoir le vecteur nul.
Ainsi, le sous-ensemble des fonctions valant 1 en 0, n'est pas un
espace vectoriel pour l'addition et la multiplication usuelle, puisque
la fonction nulle n'en fait pas partie.
Pour information et par souci de complétude, donnons la définition
exacte et précise et abstraite3.1 de la notion d'espace vectorielle:
Définition 3.1.1
Soit E, un ensemble abstrait, muni d'une opération interne notée '+'
et d'une opération externe notée '.' avec un scalaire réel
(resp. complexe).
On dit que
(E,' + ','.') possède une structure d'espace vectoriel sur
 R (resp. sur
R (resp. sur
 C) si les conditions suivantes sont
satisfaites :
C) si les conditions suivantes sont
satisfaites :
-
∀
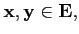
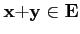
-
∀
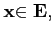 ∀λ∈
∀λ∈ R (resp.
∈
R (resp.
∈ C),
λ.
C),
λ.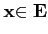
-
∀
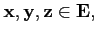 (
(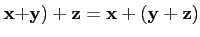
-
∀
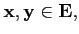
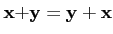
-
∀
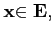 ∀λ, μ∈
∀λ, μ∈ R (resp.
∈
R (resp.
∈ C),
λμ.
C),
λμ.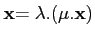
-
∀
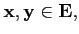 ∀λ∈
∀λ∈ R (resp.
∈
R (resp.
∈ C),
λ.(
C),
λ.(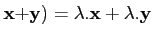
-
∀
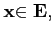 ∀λ, μ∈
∀λ, μ∈ R (resp.
∈
R (resp.
∈ C),
(λ + μ).
C),
(λ + μ).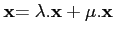
- Il existe
0E∈E tel que
∀
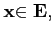
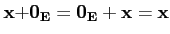
-
∀
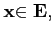 ∃
∃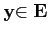 tel que
tel que
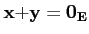
Un élément d'un espace vectoriel est appelé vecteur, et nous
choisissons de le noter avec une flèche.
Remarquons que la notion espace vectoriel est une notion de structure
d'un ensemble muni d'opérateurs. On désigne usuellement de manière
abusive (mais sans ambiguïté) l'espace vectoriel
(E,' + ','.') tout
simplement par E, car les opérations interne (addition) et externe
(multiplication par un scalaire) sont généralement implicites et ne
nécessitent pas d'être rappelées.
C'est bien ce que nous indiquions dans la sous-section précédente: un
espace vectoriel est en gros un ensemble pour lequel est défini une
addition et une multiplication par un scalaire.
Remarque 3.1.3
On a naturellement une définition analogue pour les sous-espaces
d'espaces vectoriels complexe.
Par exemple, toute droite de
 R2 passant par 0 est un
sous-espace vectoriel de
R2 passant par 0 est un
sous-espace vectoriel de
 R2 ou encore toute droite ou
tout plan de
R2 ou encore toute droite ou
tout plan de
 R3 passant par 0 est un sous-espace
vectoriel de
R3 passant par 0 est un sous-espace
vectoriel de
 R3.
R3.
Soit E un espace vectoriel (réel ou complexe) et soient p vecteurs
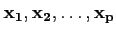 . Si
α1,..., αp sont des scalaires, alors on dit que le
vecteur
. Si
α1,..., αp sont des scalaires, alors on dit que le
vecteur
α1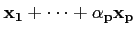
est une combinaison linéaire des vecteurs
 .
.
Définition 3.1.4
On dit que les vecteurs
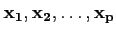 forment une famille libres, ou bien qu'ils sont linéairement
indépendants si toute combinaison linéaire non nulle de ces vecteurs
est nécessairement non nulle:
forment une famille libres, ou bien qu'ils sont linéairement
indépendants si toute combinaison linéaire non nulle de ces vecteurs
est nécessairement non nulle:
Si
α1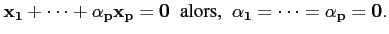
Définition 3.1.5
On dit que p vecteurs
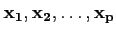 sont liés si ils ne sont pas libres.
sont liés si ils ne sont pas libres.
Proposition 3.1.6
Soit
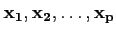 une famille de p
vecteurs. Si ces vecteurs sont libres (ou linéairement
indépendants), alors la décomposition de
une famille de p
vecteurs. Si ces vecteurs sont libres (ou linéairement
indépendants), alors la décomposition de
est unique.
Soient E1 et E2 deux espaces vectoriels réels (resp.
complexes). On définit l'espace produit par l'ensemble
On
munit cet espace produit d'une addition et d'une multiplication
induite par celles de E1 et de E2 :
Munis de ces opérations linéaires, l'espace produit
E1×E2 est encore un espace vectoriel réel (resp. complexe).
Ainsi, par exemple on note
 R2 =
R2 =  R×
R× R
et par récurrence :
R
et par récurrence :
 Rn
Rn =
 R
R×
 Rn-1
Rn-1 ∀
n = 2, 3,...
Cas des espaces
 Rn et des espaces
vectoriels réels de dimension finie
Rn et des espaces
vectoriels réels de dimension finie
Définition 3.1.7
On dit qu'un espace vectoriel E est de dimension k s'il
possède une famille libre de k vecteurs et que toute famille de
k + 1 vecteurs est lié.
Définition 3.1.8
On dit qu'une famille B de vecteurs de E est génératrice ou
encore que cette famille engendre E si tout vecteur de E est une
combinaison linéaire des vecteurs de B.
Définition 3.1.9
Une base d'un espace vectoriel E est une famille libre et
génératrice, c'est-à-dire qu'une base est constituée d'une famille de
vecteurs linéairement indépendants et qui engendre E.
Ainsi, si
B = (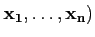 est une base de E
alors tout vecteur
est une base de E
alors tout vecteur  de E se décompose de manière unique en une combinaison linéaire des vecteurs de la base B :
de E se décompose de manière unique en une combinaison linéaire des vecteurs de la base B :
Les coefficients
α1,..., αn sont les coordonnées
de  dans la base B.
dans la base B.
Par exemple, la base de
 Rn est constituée des vecteurs
Rn est constituée des vecteurs
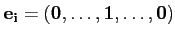 , dont toutes les coordonnées sont
nulles sauf la ieme qui vaut 1.
, dont toutes les coordonnées sont
nulles sauf la ieme qui vaut 1.
Si
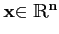 avec
avec
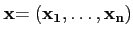 ,
alors
,
alors
La base
(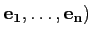 est appelée base
canonique de
est appelée base
canonique de
 Rn.
Rn.
On a alors de cette façon :
Théorème 3.1.10
L'espace
 R est de dimension n. On note
dim
R est de dimension n. On note
dim
 Rn = n.
Rn = n.
Théorème 3.1.11
Tout espace vectoriel de dimension n est isomorphe à
 Rn.
Rn.
Théorème 3.1.12
Soit E un espace vectoriel de dimension n.
- Une famille de n vecteurs de E engendre E si et
seulement si c'est une famille libre.
- E possède au moins une base et toute base est constitué de
n vecteurs.
- Si
Y = (
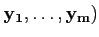 (
1≤m≤n) est
un système libre de E, alors il existe une base de E contenant
ce système. Autrement dit, on peut toujours compléter une famille
libre en une base.
(
1≤m≤n) est
un système libre de E, alors il existe une base de E contenant
ce système. Autrement dit, on peut toujours compléter une famille
libre en une base.
choi
2008-12-22
![]() C.
Cependant, dans ce cas, on peut distinguer deux possibilités :
C.
Cependant, dans ce cas, on peut distinguer deux possibilités :
![]() C en tant qu'espace vectoriel complexe, ou bien
C en tant qu'espace vectoriel complexe, ou bien
![]() C en
tant qu'espace vectoriel réel (on parle de plan complexe pour cette
dernière).
C en
tant qu'espace vectoriel réel (on parle de plan complexe pour cette
dernière).
![]() R (resp. sur
R (resp. sur
![]() C) si les conditions suivantes sont
satisfaites :
C) si les conditions suivantes sont
satisfaites :
![]() . Si
α1,..., αp sont des scalaires, alors on dit que le
vecteur
. Si
α1,..., αp sont des scalaires, alors on dit que le
vecteur
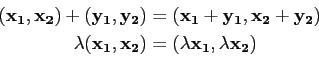
![]() R2 =
R2 = ![]() R×
R×![]() R
et par récurrence :
R
et par récurrence :
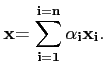
![]() Rn est constituée des vecteurs
Rn est constituée des vecteurs
![]() , dont toutes les coordonnées sont
nulles sauf la ieme qui vaut 1.
, dont toutes les coordonnées sont
nulles sauf la ieme qui vaut 1.
![]() avec
avec
![]() ,
alors
,
alors