Sous-sections
Application linéaire
Dans toute la suite, sauf indication contraire, un espace vectoriel
désignera un espace vectoriel réel.
Définition 3.2.1
Une application A d'un espace vectoriel E vers un espace vectoriel
F est une application linéaire si
-
A(
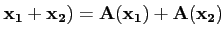 pour tout
pour tout
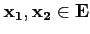 .
.
-
A(α
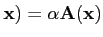 pour tout
pour tout
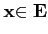 et tout scalaire α.
et tout scalaire α.
Pour désigner une application linéaire, on lit parfois
homomorphisme, dans un langage plus savant3.2.
On note souvent A , l'image d'un vecteur
, l'image d'un vecteur  par une
application linéaire A, au lieu de
A(
par une
application linéaire A, au lieu de
A(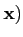 . C'est
essentiellement parce qu'en représentation matricielle (voir plus
loin) l'application ou la composition s'assimile à un produit de
matrice.
. C'est
essentiellement parce qu'en représentation matricielle (voir plus
loin) l'application ou la composition s'assimile à un produit de
matrice.
Remarquons que si A est une application linéaire alors on a nécessairement
A(
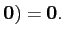
Proposition 3.2.2
Une application linéaire
est entièrement déterminée par les images des vecteurs d'une base.
En effet, si
(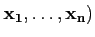 est une base de E
alors tout vecteur
est une base de E
alors tout vecteur  se décompose de manière unique
se décompose de manière unique
Alors la linéarité de A permet de calculer
A(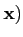 à partir des
vecteurs
A(
à partir des
vecteurs
A(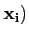 :
:
A(
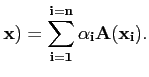
Une application linéaire d'un espace vectoriel E à image dans E
est appelée opérateur linéaire sur E (on lit aussi
endomorphisme sur E).
Définition 3.2.3
Si A est un opérateur linéaire sur E qui établit une bijection de
E vers E, on dit que A est inversible. On peut alors
définir l'application réciproque A-1 de E vers E par la
relation
A-1(
A
On a également
A(A-1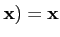 et A-1 est linéaire.
et A-1 est linéaire.
Théorème 3.2.4
Soit A un opérateur linéaire sur un espace vectoriel de dimension
finie E, alors les conditions suivantes sont équivalentes
- A est injectif
- A est surjectif
- A est bijectif
Preuve en annexe 1.7.1.
Signalons tout de même que ce théorème n'est plus vrai si E est de
dimension infinie: pensez à l'espace vectoriel des suites numériques
et l'application qui enlève le premier élément de la
suite3.3 qui est une
application surjective de l'espace des suites vers lui même mais qui
n'est pas injective puisque le noyau n'est pas réduit à 0, c'est à
dire la suite infinie de 0..
Encore quelques définitions :
Définition 3.2.5
On note
 L(E, F) l'ensemble des applications linéaires
d'un espace vectoriel E vers une espace vectoriel F.
L(E, F) l'ensemble des applications linéaires
d'un espace vectoriel E vers une espace vectoriel F.
Dans le cas des opérateurs linéaires, au lieu de
 L(E, E) on
écrit plus simplement
L(E, E) on
écrit plus simplement
 L(E).
L(E).
Si A1 et A2 sont dans
 L(E, F) et si
α1 et
α2 sont deux scalaires, on définit l'application
α1A1 + α2A2 par
L(E, F) et si
α1 et
α2 sont deux scalaires, on définit l'application
α1A1 + α2A2 par
(
α1A1 +
α2A2)
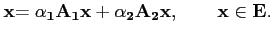
 L(E, F).
L(E, F).
Définition 3.2.6
Si E, F et Z sont trois espaces vectoriels et si
A∈ L(E, F),
B∈
L(E, F),
B∈ L(F, Z), on définit leur produit BA
comme étant la composée de A et B :
L(F, Z), on définit leur produit BA
comme étant la composée de A et B :
(
BA)
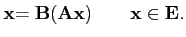
 L(E, Z).
L(E, Z).
Soulignons que même si
E = F = Z, le produit d'opérateurs linéaires ne commute pas, i.e.
AB≠BA en général.
Définition 3.2.7
Pour
A∈ L(
L( Rn,
Rn, Rm), on peut définir
une norme de A par le sup de tous les vecteurs
| A
Rm), on peut définir
une norme de A par le sup de tous les vecteurs
| A |
quand
|
quand  parcourt la boule unité de
parcourt la boule unité de
 Rn centrée en
0 :
Rn centrée en
0 :
|
A| =
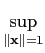
|
A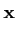
|.
Par linéarité, on a alors toujours l'inégalité :
|
A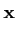
|≤|
A||
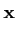
|.
Théorème 3.2.8
- Si
A∈
 L(
L( Rn,
Rn, Rm) alors
| A| < + ∞ et A est une application uniformément
continue sur
Rm) alors
| A| < + ∞ et A est une application uniformément
continue sur
 Rn.
Rn.
- Si
A, B∈
 L(
L( Rn,
Rn, Rm) et si
α est un scalaire alors
Rm) et si
α est un scalaire alors
|
A+
B|≤|
A| + |
B| |
αA| =
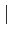 α
α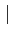
|
A|.
- Si
A∈
 L(
L( Rn,
Rn, Rm) et
B∈
Rm) et
B∈ L(
L( Rm,
Rm, Rp) alors
Rp) alors
| BA|≤| A|| B|.
Preuve en annexe 1.7.2.
- On note
 Rn[X] l'ensemble des polynômes réels de
degré ≤n.
Rn[X] l'ensemble des polynômes réels de
degré ≤n.
- L'espace des fonctions définies sur un intervalle de
 R
(c'est un e.v. de dimension infinie)
R
(c'est un e.v. de dimension infinie)
- L'ensemble des applications linéaires de
 Rn dans
Rn dans
 Rm.
Rm.
- L'espace des matrices n×m (de dimension mn).
- L'ensemble des solutions d'une équation différentielle ordinaire
homogène linéaire à coefficients constants ou non (dimension finie).
- L'ensemble des solutions d'une équation aux dérivée partielles
linéaires homogène.
Exercice : Pour chacun de ces exemples donner un sous-espace vectoriel.
choi
2008-12-22
![]() , l'image d'un vecteur
, l'image d'un vecteur ![]() par une
application linéaire A, au lieu de
A(
par une
application linéaire A, au lieu de
A(![]() . C'est
essentiellement parce qu'en représentation matricielle (voir plus
loin) l'application ou la composition s'assimile à un produit de
matrice.
. C'est
essentiellement parce qu'en représentation matricielle (voir plus
loin) l'application ou la composition s'assimile à un produit de
matrice.
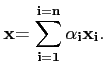
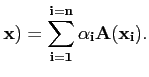
![]() L(E, F) et si
α1 et
α2 sont deux scalaires, on définit l'application
α1A1 + α2A2 par
L(E, F) et si
α1 et
α2 sont deux scalaires, on définit l'application
α1A1 + α2A2 par