Sous-sections
Matrice d'une application linéaire
Soient X et Y deux espaces vectoriels de
dimension respective n et m.
Soient
(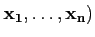 et
(
et
(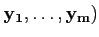 deux bases respectives de X et Y. Toute application
linéaire
A∈
deux bases respectives de X et Y. Toute application
linéaire
A∈ L(X, Y) détermine un ensemble de coefficients
notés aij tels que
L(X, Y) détermine un ensemble de coefficients
notés aij tels que
A(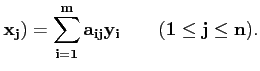 |
(3.1) |
Il est usuel et commode de
représenter ces coefficients dans un tableau rectangulaire de m
lignes et de n colonnes appelé matrice m×n noté
M(A)3.4, on parle alors de représentation matricielle de l'application linéaire :
M(
A) =
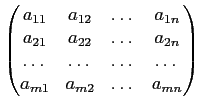
.
Remarquons que les coordonnées aij du vecteur
A(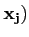 apparaissent dans la jème colonne de la matrice M(A). Les
vecteurs
A(
apparaissent dans la jème colonne de la matrice M(A). Les
vecteurs
A(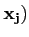 sont donc parfois appelés vecteurs
colonnes de la matrice M(A).
sont donc parfois appelés vecteurs
colonnes de la matrice M(A).
On appelle rang de A, la dimension de l'image de X par
A. Il est donc égal à la dimension de l'espace engendré par le
vecteurs colonnes de M(A).
A l'aide des coefficients de la matrice on peut déterminer l'image de
tout vecteur  de X par A. En effet, si
de X par A. En effet, si
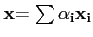 , on déduit par linéarité de A que
, on déduit par linéarité de A que
A(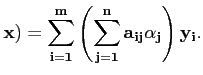 |
(3.2) |
Réciproquement, donnons nous maintenant une matrice m×n de
coefficients aij, notée M(A). Si on définit l'application A
par la formule (1.2), on remarque que
A∈ L(X, Y),
où nous rappelons que X et Y sont des espaces vectoriels de
dimension n et m respectivement.
Ainsi :
L(X, Y),
où nous rappelons que X et Y sont des espaces vectoriels de
dimension n et m respectivement.
Ainsi :
Théorème 3.3.1
Il y a une bijection entre
 L(X, Y) et l'ensemble des matrice
m×n,
L(X, Y) et l'ensemble des matrice
m×n,
- m lignes, dimension de l'espace d'arrivée,
- n colonnes, dimension de l'espace de départ.
Exemple : Plaçons nous dans
 R2 et
R2 et
 R3, si
relativement à des bases
(
R3, si
relativement à des bases
( et
(
et
(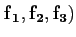 , une application linéaire est
définie comme
, une application linéaire est
définie comme
Alors, la matrice de l'application linéaire A dans les bases
considérées s'écrit :
A =
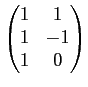
.
Ainsi, si par exemple
alors
A(
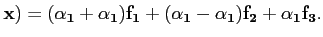
Ce qu'on note également noter sous la forme:
A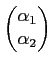
=
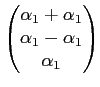
.
Enchaînons par un résultat fondamental:
Théorème 3.3.2
Soit X un espace vectoriel réel de dimension finie. Étant donné une
base de X, on peut définir le produit scalaire :
∀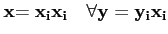
Ainsi pour tout
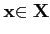 , on défini une forme linéaire sur
X. Réciproquement, toute forme linéaire sur X, via sa
représentation matricielle, peut être présentée comme un produit
scalaire par un vecteur de X.
, on défini une forme linéaire sur
X. Réciproquement, toute forme linéaire sur X, via sa
représentation matricielle, peut être présentée comme un produit
scalaire par un vecteur de X.
Il existe donc une bijection entre
 L(X,
L(X, R) et X.
R) et X.
Corollaire 3.3.3
Dans le cas où
X =  Rn le produit scalaire rapporté à la
base canonique définit la bijection naturelle entre
Rn le produit scalaire rapporté à la
base canonique définit la bijection naturelle entre
 L(
L( Rn,
Rn, R) et
R) et
 Rn.
Rn.
Cette bijection est essentielle pour bien comprendre le calcul différentiel:
Ainsi un réel a peut être identifié à une forme linéaire réelle définit par
l'application qui associe à tout réel x, la valeur ax.
De même un vecteur
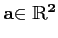 peut être identifié à
forme linéaire réelle définit par l'application qui associe à tout
vecteur
peut être identifié à
forme linéaire réelle définit par l'application qui associe à tout
vecteur  , la valeur réelle
, la valeur réelle
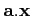 .
.
Terminons cette section par une proposition permettant d'obtenir une
estimation de la norme d'une application linéaire grâce à sa
représentation matricielle
Proposition 3.3.4
Soit aij les coefficients de la matrice de
A∈ L(X, Y) de
la base
(
L(X, Y) de
la base
(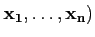 de X dans
(
de X dans
(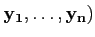 de Y. On a la majoration :
de Y. On a la majoration :
Preuve en annexe 1.7.3
Considérons à présent un troisième espace vectoriel Z de dimension
p avec une base
(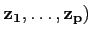 . Si A est
définie par (1.1), définissons de la même manière une
application linéaire
B∈
. Si A est
définie par (1.1), définissons de la même manière une
application linéaire
B∈ L(Y, Z) à l'aide de coefficients
bki :
L(Y, Z) à l'aide de coefficients
bki :
B(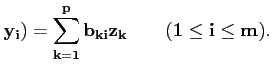 |
(3.3) |
On peut alors définir l'application composée
BA∈ L(X, Z) par
L(X, Z) par
(
BA)(
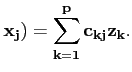
on a finalement
(
BA)(
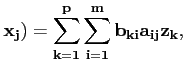
ckj = 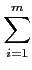 bkiaij. bkiaij. |
(3.4) |
On dit aussi que la matrice p×n, notée C, de coefficients
ckj est le produit de la matrice A par la matrice B.
La formule (1.4) donne la règle usuelle du produit de
deux matrices.
Terminons par la règle : le produit d'une matrice
n×m par une matrice
m×p, donne une matrice
n×p.
(n×m)(m×p) = (n×p).
Si les dimensions des espaces ne rentrent pas dans le cadre de cette
règle, le produit n'est pas défini, les dimensions d'espaces étant incompatibles.
Changement de bases et Matrices de passage
Dans la pratique, et notamment en Mécanique, il apparaît souvent judicieux
de passer d'un système de coordonnées à un autre suivant les besoins.
Il est donc nécessaire de maîtriser les outils permettant ces passages.
Soit X un espace vectoriel de dimension n et soit un vecteur
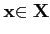 de coordonnées
αi dans la base
(
de coordonnées
αi dans la base
(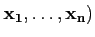 . Soit
(
. Soit
(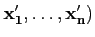 une autre base de
X. Supposons connues les coordonnées des vecteurs
une autre base de
X. Supposons connues les coordonnées des vecteurs
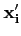 dans la base
(
dans la base
(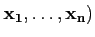 :
:
On a donc défini une matrice P représentant l'application
identité de X, muni
de la base
(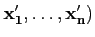 , dans
X, muni de la base
(
, dans
X, muni de la base
(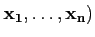 :
:
IdX(
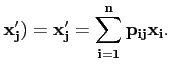
Théorème 3.3.5
La matrice P ayant pour jème colonne les coordonnées de
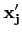 dans la base
(
dans la base
(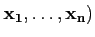 est
inversible. On l'appelle la matrice de passage de la base
(
est
inversible. On l'appelle la matrice de passage de la base
(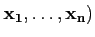 vers la base
(
vers la base
(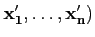 .
.
De plus, si
αi sont les ``anciennes'' coordonnées de
 dans
(
dans
(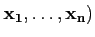 , formant la matrice
colonne (n×1)
[
, formant la matrice
colonne (n×1)
[![$ \bf{x}{]_{x}$](img110.png) , on peut les exprimer en
fonction des ``nouvelles'' coordonnées
α′j de
, on peut les exprimer en
fonction des ``nouvelles'' coordonnées
α′j de  dans
(
dans
(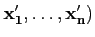 , notées
également par une matrice colonne
[
, notées
également par une matrice colonne
[![$ \bf{x}{]_{x^{\prime}}$](img111.png) avec la formule :
avec la formule :
[
![$\displaystyle \bf{x}{]_{x}= P [\vec{x}]_{x^{\prime}} \quad \iff
\quad P^{-1}[\vec{x}]_{x}=[\vec{x}]_{x^{\prime}}.$](img112.png)
alors
αi =
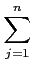 pijα′j
pijα′j.
Autrement dit, pour obtenir les ``nouvelles'' coordonnées en
fonction des anciennes, il faut passer par la matrice de passage
P-1 de la base
(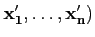 vers la base
(
vers la base
(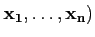 .
.
La notation P-1 est justifiée par le fait que P-1 est
nécessairement la matrice inverse de P. En effet, on doit avoir
PP-1 = P-1P = In,
où In est la matrice identité n×n.
Considérons maintenant une application linéaire
A∈ L(X, Y)
où X et Y sont toujours des espaces vectoriels de dimension n et
m respectivement.
L(X, Y)
où X et Y sont toujours des espaces vectoriels de dimension n et
m respectivement.
On muni X des bases
(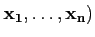 et
(
et
(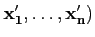 , avec P la
matrice de passage de
(
, avec P la
matrice de passage de
(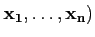 vers
(
vers
(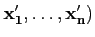 .
.
On muni de même
Y des bases
(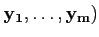 et
(
et
(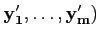 , avec Q la
matrice de passage de
(
, avec Q la
matrice de passage de
(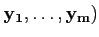 vers
(
vers
(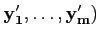 . Alors, on a la
proposition :
. Alors, on a la
proposition :
Proposition 3.3.6
Soit M la matrice de A de la base
(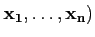 de X vers la base
(
de X vers la base
(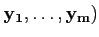 de Y. Alors la matrice
M′ de A de la base
(
de Y. Alors la matrice
M′ de A de la base
(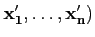 de X vers la
base
(
de X vers la
base
(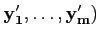 de Y, se
décompose :
de Y, se
décompose :
M′ = Q-1MP.
Preuve.
En effet, on a
et

Dans le cas particulier où A est un opérateur linéaire (on dit aussi
endomorphisme) sur X, si P est la matrice de passage de
la base
(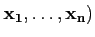 vers la base
(
vers la base
(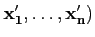 , alors si M et
M′ sont les matrices de A dans
(
, alors si M et
M′ sont les matrices de A dans
(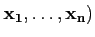 et
(
et
(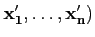 respectivement,
alors on a
respectivement,
alors on a
M′ = P-1MP.
choi
2008-12-22
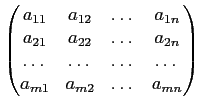 .
.
![]() de X par A. En effet, si
de X par A. En effet, si
![]() , on déduit par linéarité de A que
, on déduit par linéarité de A que
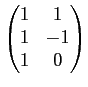 .
.
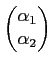 =
= 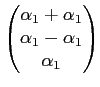 .
.
![]() L(X,
L(X,![]() R) et X.
R) et X.![]() peut être identifié à
forme linéaire réelle définit par l'application qui associe à tout
vecteur
peut être identifié à
forme linéaire réelle définit par l'application qui associe à tout
vecteur ![]() , la valeur réelle
, la valeur réelle
![]() .
.
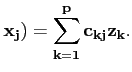
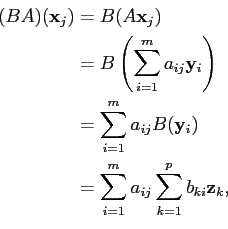
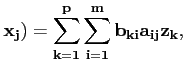
![]() de coordonnées
αi dans la base
(
de coordonnées
αi dans la base
(![]() . Soit
(
. Soit
(![]() une autre base de
X. Supposons connues les coordonnées des vecteurs
une autre base de
X. Supposons connues les coordonnées des vecteurs
![]() dans la base
(
dans la base
(![]() :
:
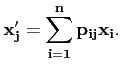
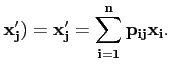

![]() L(X, Y)
où X et Y sont toujours des espaces vectoriels de dimension n et
m respectivement.
L(X, Y)
où X et Y sont toujours des espaces vectoriels de dimension n et
m respectivement.
![]() et
(
et
(![]() , avec P la
matrice de passage de
(
, avec P la
matrice de passage de
(![]() vers
(
vers
(![]() .
.
![]() et
(
et
(![]() , avec Q la
matrice de passage de
(
, avec Q la
matrice de passage de
(![]() vers
(
vers
(![]() . Alors, on a la
proposition :
. Alors, on a la
proposition :